Rozwiązanie łamigłówki dla czterech krążków

Wieże Hanoi – problem polegający na odbudowaniu, z zachowaniem kształtu, wieży z krążków o różnych średnicach (popularna dziecięca zabawka), przy czym podczas przekładania wolno się posługiwać buforem (reprezentowanym w tym przypadku przez dodatkowy słupek), jednak przy ogólnym założeniu, że nie wolno kłaść krążka o większej średnicy na mniejszy ani przekładać kilku krążków jednocześnie. Jest to przykład zadania, którego złożoność obliczeniowa wzrasta niezwykle szybko w miarę zwiększania parametru wejściowego, tj. liczby elementów wieży.

Pochodzenie

Zagadka Wież Hanoi stała się znana w XIX wieku dzięki matematykowi Édouard Lucasowi , który proponował zagadkę dla 8 krążków. Do sprzedawanego zestawu była dołączona (prawdopodobnie wymyślona przez Lucasa) tybetańska legenda , według której mnisi w świątyni Brahmy rozwiązują tę łamigłówkę dla 64 złotych krążków. Legenda mówi, że gdy mnisi zakończą zadanie, nastąpi koniec świata. Zakładając, że wykonują 1 ruch na sekundę, ułożenie wieży zajmie 2⁶⁴−1 = 18 446 744 073 709 551 615 (blisko 18 i pół tryliona ) sekund, czyli około 584 542 miliardów lat. Dla porównania: Wszechświat ma około 13,7 mld lat.

Algorytm

Od lewej: słupek A z całą wieżą, pusty słupek B pełniący rolę bufora i pusty słupek docelowy C

Wieże Hanoi można łatwo rozwiązać za pomocą prostego algorytmu rekurencyjnego lub iteracyjnego.

• Oznaczmy kolejne słupki literami A, B i C.
• Niech n będzie liczbą krążków, które chcemy przenieść ze słupka A na słupek C posługując się słupkiem B jako buforem.

Rozwiązanie rekurencyjne

Algorytm rekurencyjny składa się z następujących kroków:

1. przenieś (rekurencyjnie) n-1 krążków ze słupka A na słupek B posługując się słupkiem C,
2. przenieś jeden krążek ze słupka A na słupek C,
3. przenieś (rekurencyjnie) n-1 krążków ze słupka B na słupek C posługując się słupkiem A

Przykładowe implementacje

• w Pythonie :

def hanoi(n, A, B, C):    """słupki A, B, C są listami"""    if n > 0:        hanoi(n-1, A, C, B)        C.insert(0, A.pop(0))        hanoi(n-1, B, A, C)

• w C++ :

#include <iostream>using namespace std; void hanoi(int n, char A, char B, char C) {// przekłada n krążków z A korzystając z B na C  if (n > 0) {    hanoi(n-1, A, C, B);    cout << A << " -> " << C << endl;    hanoi(n-1, B, A, C);  }} int main(int argc, char *argv[]) {  hanoi(3, 'A', 'B', 'C');  return 0;}

Algorytm rozwiązywania wież Hanoi jest klasycznym przykładem algorytmu rekurencyjnego używanego w nauczaniu informatyki .

Rozwiązanie iteracyjne

Algorytm iteracyjny składa się z następujących kroków:

1. przenieś najmniejszy krążek na kolejny (*) słupek.
2. wykonaj jedyny możliwy do wykonania ruch, nie zmieniając położenia krążka najmniejszego
3. powtarzaj punkty 1 i 2, aż do odpowiedniego ułożenia wszystkich krążków.

(*) Kolejny słupek wyznaczamy w zależności od liczby krążków. Jeśli liczba krążków jest parzysta, kolejnym słupkiem jest ten po prawej stronie (gdy dojdziemy do słupka C w następnym ruchu używamy słupka A). Natomiast jeśli liczba krążków jest nieparzysta, kolejnym słupkiem jest ten po lewej stronie (gdy dojdziemy do słupka A w następnym ruchu używamy słupka C)

Najmniejsza liczba wymaganych ruchów

Równanie określające liczbę ruchów potrzebnych do rozwiązania problemu wież Hanoi dla n krążków:

Dowód

Łatwo pokazać, że :

• w pierwszym kroku przekładamy n-1 krążków na jeden słupek (bez straty ogólności załóżmy, że jest to krążek nr 3) - wymaga to co najmniej L(n-1) ruchów
• przekładamy n-ty krążek na drugi słupek - wymaga to jednego ruchu
• przekładamy pozostałe krążki ze słupka 3. na n-ty krążek leżący na 2. słupku - wymaga to co najmniej L(n-1) ruchów

a więc .

Aby wykazać, że można przeprowadzić następujące rozumowanie:

Aby móc ruszyć n-ty krążek, trzeba najpierw zdjąć wszystkie leżące na nim krążki, tak by po ich zdjęciu jeden z słupków pozostał wolny (aby na jego "dno" mógł trafić n-ty krążek). A więc ze słupka 1 przekładamy krążki na słupek 3. Ponieważ aż do momentu gdy na drążku 1 pozostanie tylko n-ty krążek nie ma znaczenia czy rzeczywiście się on tam znajduje, a więc do tego momentu sytuacja upraszcza się do rozwiązania problemu wież Hanoi dla n-1 krążków (którego minimalna liczba ruchów wynosi L(n-1)). Na przełożenie krążka n-tego potrzeba co najmniej jeden ruch. Po jego przełożeniu znów potrzeba przełożyć krążki - jest to oczywiście znów sytuacja n-1 krążków (wymagająca co najmniej L(n-1) ruchów).

A więc

co w połączeniu z górnym ograniczeniem na L(n) daje równość

Postać jawna wzoru na liczbę ruchów

Powyższe równanie rekurencyjne można w łatwy sposób przekształcić do postaci jawnej, tj. nie korzystającej z rekursji:

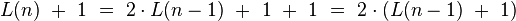
Niech

Wtedy

jest to równanie określające ciąg geometryczny o ilorazie równym 2 takie, że

Po powrocie do L(n) otrzymujemy

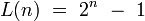
Zastosowanie

Mimo swojego wieku łamigłówka jest stale tematem prac matematyków i znane są jej bardziej rozbudowane wersje np. z więcej niż trzema słupkami.

W psychologii łamigłówka ta jest jednym z testów na kojarzenie.

Zobacz też

• rekurencja .