Przekształcenie afiniczne, powinowactwo lub pokrewieństwo – przekształcenie geometryczne przestrzeni euklidesowych odwzorowujące odcinki na odcinki. Są one homomorfizmami przestrzeni afinicznych , będących uogólnieniem przestrzeni euklidesowych, czyli spełniają one analogiczną rolę, co przekształcenia liniowe względem przestrzeni liniowych (również będących uogólnieniem przestrzeni euklidesowych).

W poniższym artykule powinowactwo będzie oznaczać przekształcenie przestrzeni euklidesowych, zaś przekształcenie afiniczne będzie odnosiło się do odwzorowania przestrzeni afinicznych; pokrewieństwa będą oznaczać dowolne z tych przekształceń.

Definicja geometryczna

Powinowactwem lub pokrewieństwem nazywamy różnowartościowe przekształcenie przestrzeni euklidesowych, które odwzorowuje proste na proste ( kolineacja ). Tę definicję można wyrazić elementarnie (czyli nie w języku zbiorów):

Dla każdych trzech różnych współliniowych punktów p₁,p₂,p₃ ich obrazy odpowiednio q₁,q₂,q₃ także będą (różnymi) współliniowymi punktami.

Powinowactwo zachowuje relację leżenia między, więc obrazem odcinka jest odcinek. W szczególności oznacza, że obrazem punktu wewnętrznego dowolnego odcinka jest punkt wewnętrzny obrazu odcinka.

Ostatnia własność ma ciekawe i ważne wzmocnienie: powinowactwo zachowuje stosunek podziału odcinka dowolnym punktem wewnętrznym. Jeśli więc jest punktem wewnętrznym odcinka to

gdzie są obrazami odpowiednich punktów oraz ρ jest odległością (metryką).

Definicja algebraiczna

Przekształcenie nazywa się afinicznym, jeżeli jest postaci

,

gdzie f jest pewnym przekształceniem liniowym , nazywanym częścią liniową tego odwzorowania, a to wektor przesunięcia . Dla przestrzeni skończonego wymiaru prawdziwy jest wzór

,

gdzie jest macierzą wspomnianego przekształcenia liniowego.

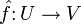Inaczej definicję tę można wysłowić następująco: niech A,B będą przestrzeniami afinicznymi stowarzyszonymi odpowiednio z przestrzeniami liniowymi V,U. Odwzorowanie nazywa się afinicznym, jeżeli istnieje punkt , że przekształcenie , nazywane częścią liniową f, dane wzorem jest liniowe .

Reprezentacja

Standardowa algebra wektorowa wykorzystuje macierze do reprezentowania przekształceń liniowych (przestrzeni skończeniewymiarowych) oraz dodawanie wektorów do reprezentowania przesunięć. Wykorzystując pojęcie macierzy rozszerzonej można reprezentować oba te rodzaje przekształceń za pomocą mnożenia macierzy . Metoda ta wymaga powiększenia wektorów tak, by na ostatniej ich współrzędnej znalazła się jedynka i wszystkich macierzy o dodatkowy wiersz zerowy na jej dole, dodatkową kolumnę – wektor przesunięcia – po jej prawej stronie, przy czym prawy dolny element (leżący na przecięciu dodatkowych kolumny i wiersza) był równy jedności. Zatem, w zapisie klatkowym , jeśli A jest macierzą, to

jest równoważne zapisowi

.

Zwykłe mnożenie macierzy przez wektor zawsze przekształca początek na początek, zatem nigdy nie może reprezentować przesunięcia, w którym początek musi być przekształcony na pewien inny punkt. Dodanie jedynki na końcu każdego wektora powoduje w istocie rozpatrywanie danej przestrzeni jako podzbioru przestrzeni o wymiar większej. Początek oryginalnej przestrzeni znajduje się w punkcie 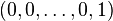. Przesunięcie oryginalnej przestrzeni w przestrzeni wyższego wymiaru jest wówczas możliwe (możliwe jest w szczególności powinowactwo osiowe ). Metoda ta jest przykładem zastosowania współrzędnych jednorodnych .

Zaletą korzystania ze współrzędnych jednorodnych jest możliwość złożenia dowolnej liczby przekształceń afinicznych poprzez mnożenie macierzy (zob. niżej). Znajduje to zastosowanie w grafice komputerowej.

Własności

Przekształcenia afiniczne płaszczyzny (przestrzeni) w siebie obejmują m.in.

• izometrie : przesunięcia równoległe , obroty , symetrie środkowe , symetrie osiowe , symetrie płaszczyznowe , symetrie z obrotem (symetrie spiralne), symetrie z poślizgiem ,
• podobieństwa : jednokładności (homotetie lub skalowania), dylatacje ,
• powinowactwa osiowe , powinowactwa prostokątne, symetrie skośne , obroty eliptyczne, obroty hiperboliczne.

Wszystkie powyższe przekształcenia są liniowe , przy czym w szczególności przekształcenie afiniczne może być złożeniem dowolnej liczby powyższych odwzorowań. Ponieważ złożenie przekształceń afinicznych jest afiniczne, a jako bijekcje (wzajemnie jednoznaczne) są one odwracalne, to zbiór wszystkich przekształceń wraz ze składaniem przekształceń jest grupą .

Dowolne przekształcenie afiniczne płaszczyzny jest powinowactwem osiowym lub złożeniem co najwyżej 3 powinowactw osiowych.

Dowolne przekształcenie afiniczne przestrzeni jest powinowactwem płaszczyznowym lub złożeniem co najwyżej 4 powinowactw płaszczyznowych.

Zachowywane przy pokrewieństwach własności figur geometrycznych nazywa się niezmiennikami afinicznymi; przykładami mogą być równoległość prostych, zachowywanie stosunku długości równoległych odcinków oraz pól figur (w przestrzeni również na płaszczyznach leżących na równoległych płaszczyznach).

Niezmienniki określające jednoznacznie grupę przekształceń afinicznych:

• prosta, odcinek, wektor
• współliniowość punktów (nie dotyczy prostej),
• równoległość prostych, wypukłość figur,
• trójkąt, równoległobok,
• równość wektorów,
• stosunek długości równoległych odcinków,
• stosunek pól figur (na płaszczyźnie),
• stosunek pól figur na płaszczyznach równoległych (w przestrzeni),
• elipsa, parabola, hiperbola.

Każde przekształcenie afiniczne na płaszczyznie można przedstawić jako złożenie:

• podobieństwa i powinowactwa osiowego
• podobieństwa i powinowactwa prostokątnego
• podobieństwa i powinowactwa ścinającego
• podobieństwa i symetrii skośnej
• izometrii i dwóch powinowactw prostokątnych o osiach powinowactwa wzajemnie prostopadłych

Uwaga: Z definicji powinowactwa osiowego, prostokątnego lub ścinającego wynika, że może być także tożsamością, zaś szczególnym przypadkiem symetrii skośnej jest symetria osiowa.

Twierdzenia

Geometria

Istnienie przekształcenia afinicznego o zadanej części liniowej 

Dla danego przekształcenia liniowego istnieje dokładnie jedno przekształcenie afiniczne będące złożeniem tego przekształcenia liniowego i pewnego przesunięcia.

Istnienie przekształcenia afinicznego zadanego w danej bazie 

Dla danej pary trzech niewspółliniowych punktów na płaszczyźnie (czterech w przestrzeni, itp.) istnieje dokładnie jedno przekształcenie afiniczne odwzorowujące pierwszą parę na drugą.

Algebra liniowa

Istnienie przekształcenia afinicznego o zadanej części liniowej 

Niech (A,V) i (B,U) będą przestrzeniami afinicznymi wraz z dowolnie wybranymi punktami , zaś będzie przekształceniem liniowym. Istnieje wówczas dokładnie jedno przekształcenie afiniczne takie, że f(p) = q i .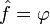

Istnienie przekształcenia afinicznego zadanego w danej bazie 

Niech dane będą przestrzenie afiniczne (A,V) i (B,U) wraz z bazami, odpowiednio . Istnieje wówczas dokładnie jedno przekształcenie afiniczne takie, że f(p₀) = q₀ oraz dla .

Literatura

• Jerzy Bednarczuk: Urok przekształceń afinicznych. Warszawa: 1978. 

Zobacz też

• ,
• przestrzeń afiniczna ,
• przekształcenie liniowe ,
• kolineacja .