Aksjomat wyboru (ozn. AC) – jeden z
aksjomatów
teorii mnogości
. Używa się różnych jego równoważnych sformułowań. Najczęściej spotykane jest następujące:
- Dla każdej rodziny
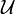niepustych
zbiorów
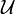rozłącznych istnieje zbiór V, do którego należy dokładnie po jednym elemencie każdego ze zbiorów z tej rodziny (zbiór taki nazywany jest selektorem). ![\bigwedge_{\mathcal{U}} \Bigg[\Big(\bigwedge _{X \in \mathcal{U}} X \neq \varnothing\Big) \land \Big(\bigwedge _{X,Z \in \mathcal{U}} \big(X \neq Z \Rightarrow X \cap Z = \varnothing\big)\Big) \implies \bigvee_V \bigwedge_{X \in \mathcal{U}} \bigvee_z \big(X \cap V= \{z\}\big)\Bigg]](http://upload.wikimedia.org/math/2/3/8/2387222a4c1b944d070363df95f1a5d4.png)
Przykładem innego sformułowania aksjomatu wyboru jest
-
iloczyn kartezjański
dowolnej liczby niepustych zbiorów jest niepusty.
Elementami iloczynu kartezjańskiego 
są funkcje 
spełniące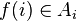 
dla każdego 
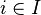. Aksjomat wyboru postuluje:
- Jeśli
jest rodziną zbiorów spełniącą warunek 
dla każdego 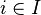, wówczas istnieje funkcja wyboru f, taka że 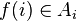dla każdego .
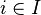Równoważne aksjomatowi wyboru są także tak zwany
lemat Kuratowskiego-Zorna
oraz twierdzenie mówiące, że każdy zbiór można
dobrze uporządkować
.
Kontrowersje
Aksjomat wyboru jest trywialny (i wynika z innych aksjomatów), jeśli zastosować go do skończonych rodzin zbiorów. W przypadku, kiedy mamy do czynienia z nieskończoną rodziną zbiorów, wydaje się również intuicyjny, lecz jego konsekwencje są zaskakujące. Na przykład
Stefan Banach
i
Alfred Tarski
korzystając z AC, udowodnili
twierdzenie o paradoksalnym rozkładzie kuli
. Mówi ono, że w
przestrzeni euklidesowej
R3 można podzielić kulę na skończoną liczbę części, z których da się złożyć dwie kule o takiej samej średnicy, co kula wyjściowa.
Obecnie większość matematyków uznaje i stosuje aksjomat wyboru. Przy twierdzeniach, których
dowód
go wykorzystuje, przyjęło się jednak zaznaczać ten fakt.
Można również rozważać
modele
teorii mnogości (tzn. aksjomatów
ZF
), w których prawdziwa jest
negacja
aksjomatu wyboru.
Słabsze formy
Czasami matematycy asekurując się przed paradoksalnymi następstwami zakładania aksjomatu wyboru, ograniczają się do jego słabszych, nierównoważnych wersji, jednak w wielu zastosowaniach wystarczających i nierzadko wygodniejszych.
Te słabsze formy są często podobne do aksjomatu wyboru i tylko ograniczają rozważane rodziny niepustych zbiorów, np. do skończonych zbiorów (ACF), albo zakładają, że funkcja wyboru wybiera podzbiór każdego danego niepustego zbioru zamiast elementu. Następujące postulaty wynikają oczywiście z ZFC:
- Dla każdego zbioru X istnieje funkcja przyporządkowująca każdemu, co najmniej dwuelementowemu podzbiorowi zbioru X pewien niepusty, właściwy podzbiór zbioru X.
- Aksjomat wyboru dla zbiorów dających się dobrze uporządkować - ACWO
- Dla każdego zbioru X istnieje funkcja przyporządkowująca dokładnie jeden element
każdemu niepustemu podzbiorowi zbioru X dającemu się dobrze uporządkować.
- Aksjomat wyboru dla zbiorów skończonych - ACF
- Dla każdego zbioru X istnieje funkcja przyporządkowująca dokładnie jeden element każdemu niepustemu, skończonemu podzbiorowi zbioru X.
- Aksjomat wyboru dla zbiorów n-elementowych - Cn
- Dla każdego zbioru X istnieje funkcja wybierająca po jednym elemencie z każdego n-elementowego podzbioru zbioru X.
- Przeliczalny aksjomat wyboru - CAC albo ACω
- Dla każdej przeliczalnej rodziny zbiorów istnieje funkcja wyboru.
Inne wersje wynikają z aksjomatu wyboru, ale mają całkowicie inną formę:
- Aksjomat liniowego uporządkowania - OP
- Każdy zbiór da się
liniowo
uporządkować.
- Każdy zbiór nieskończony da się
podzielić
na dwa nieskończone, rozłączne zbiory.
(Aksjomat ten jest bardzo słaby: na przykład nie można przy jego założeniu udowodnić, że każdy nieskończony zbiór da się podzielić na nieskończenie wiele nieskończonych rozłącznych zbiorów.)
- Zasada wyborów zależnych - PDC albo DC
- Niech X będzie niepustym zbiorem, oraz
będzie pewną
relacją
na X. Jeżeli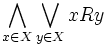
,
- wówczas istnieje ciąg (xn) elementów zbioru X, że
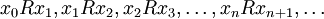
(Już podstawowe twierdzenia w
analizie
i
teorii miary
potrzebują założenia PDC albo przynajmniej CC (np. aby udowodnić, że zbiór liczb rzeczywistych nie jest sumą przeliczalnej rodziny
zbiorów miary zero
). Istnienie zbiorów
niemierzalnych
nie wynika z aksjomatów ZF+PDC, czyli układ
- ZF+PDC+"każdy podzbiór prostej rzeczywistej jest mierzalny"
jest niesprzeczny.)
- Na każdej
algebrze Boole'a
istnieje
ultrafiltr
.
(Ten aksjomat wystarczy aby udowodnić np.
twierdzenie o zwartości
,
twierdzenie Hahna-Banacha
, istnienie zbiorów niemierzalnych, i
twierdzenie Tichonowa
dla przestrzeni
T2
.)
Prawdziwe są następujące ciągi implikacji:
- AC ⇒ PDC ⇒ CAC
- AC ⇒ SP ⇒ OP ⇒ ACF ⇒ ∀n Cn ⇒ Cm ⇒ PP
- AC ⇒ BPI ⇒ OP
- AC ⇒ ACWO ⇒ ACF
Przypisy
- ↑ Nazwy skrótów pochodzą z języka angielskiego, odpowiednio od Selection Principle, Axiom of choice for well orderable sets, Axiom of choice for finite sets, Axiom of choice for finite sets of n elements, Countable axiom of choice, The Ordering Principle, Partition Principle, Principle of dependent choices, Boolean prime ideal theorem.
Bibliografia
- Omar De La Cruz, Carlos Augusto Di Prisco: Weak forms of the axiom of choice and partitions of infinite sets. Dordrecht: Kluwer Acad. Publ., 1998.
- Thomas Jech: The Axiom of Choice. Amsterdam: North Holland, 1973.
Zobacz też
