Algebra ogólna – obiekt
matematyczny
będący przedmiotem badań
algebry uniwersalnej
. Czasami algebra uniwersalna nazywana jest algebrą ogólną, wówczas rozważane w niej obiekty nazywa się zwykle algebrami abstrakcyjnymi lub po prostu algebrami.
Definicja
Niech  będzie zbiorem i niech
będzie zbiorem i niech  .
.
Algebrą sygnatury  jest para
jest para  , gdzie
, gdzie 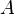 jest zbiorem (zwykle niepustym), a
jest zbiorem (zwykle niepustym), a 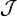 jest
funkcją
, która elementowi
jest
funkcją
, która elementowi 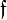 zbioru
zbioru  przyporządkowuje
przyporządkowuje  -
argumentowe
działanie
-
argumentowe
działanie
 w zbiorze
w zbiorze 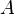 . Zbiór
. Zbiór 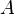 nazywamy uniwersum algebry
nazywamy uniwersum algebry  , funkcję
, funkcję 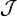 interpretacją zbioru
interpretacją zbioru  w algebrze
w algebrze  .
.
Dla danej algebry  , jego uniwersum oznacza się zazwyczaj jako
, jego uniwersum oznacza się zazwyczaj jako 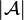 . Także zamiast pisać
. Także zamiast pisać  pisze się
pisze się  albo
albo  .
.
Przykłady
- Algebra
Peano
arytmetyki liczb naturalnych,
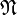 .
.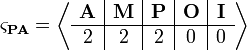 ,
,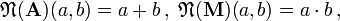
 oraz
oraz 
- Algebra
Presburgera
arytmetyki samego dodawania,
 .
. ,
,
- Algebra Cegielskiego arytmetyki samego mnożenia,
 .
. ,
,
- Algebra arytmetyki liczb całkowitych,
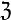 .
.
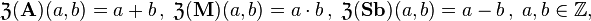
 oraz
oraz 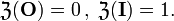
- Algebra podzbiorów zbioru
 ,
,  .
. ,
,
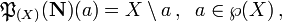 oraz
oraz 
- Krata podzielności w
 ,
,  .
. ,
,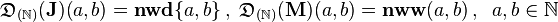 (zob.
nww
,
nwd
)
(zob.
nww
,
nwd
)
oraz 
Redukty i wzbogacenia
Niech  będzie algebrą sygnatury
będzie algebrą sygnatury  i niech
i niech  .
.
Reduktem prostym algebry  do
do  nazywamy algebrę
nazywamy algebrę  .
.
Przykłady
 i
i  są reduktami prostymi
są reduktami prostymi 
- Algebrę
 nazywamy kratą podzbiorów zbioru
nazywamy kratą podzbiorów zbioru  .
.
W niektórych wypadkach wprowadzone wyżej pojęcie reduktu prostego może być niewystarczające. Będzie tak np. w sytuacji, gdy na jednym uniwersum będziemy potrzebowali wprowadzić równolegle kilka struktur wzajemnie ze sobą powiązanych jak jest np. w przypadku
pierścieni
, czy
ciał
. Wtedy pomocnym okaże się następujące pojęcie reduktu nieprostego:
Redukty nieproste
Niech  będzie algebrą sygnatury
będzie algebrą sygnatury  i niech
i niech  będzie różnowartościowe. Reduktem nieprostym algebry
będzie różnowartościowe. Reduktem nieprostym algebry  do π nazywamy algebrę
do π nazywamy algebrę  sygnatury
sygnatury  , której uniwersum jest
, której uniwersum jest 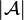 i w której
i w której

Algebra  jest wzbogaceniem (prostym) algebry
jest wzbogaceniem (prostym) algebry  , jeśli
, jeśli  jest reduktem (prostym) algebry
jest reduktem (prostym) algebry  .
.
Przykłady
Pierścień to taka algebra  sygnatury
sygnatury  , że redukt
, że redukt  jest grupą przemienną, a
jest grupą przemienną, a  jest półgrupą oraz spełnione są równości:
jest półgrupą oraz spełnione są równości:

gdzie

Tutaj zastosowana jest konwencja notacyjna wedle której  jest innym zapisem funkcji
jest innym zapisem funkcji 
Ciało to taka algebra  sygnatury
sygnatury  , że
, że  jest pierścieniem, a
jest pierścieniem, a  jest grupą.
jest grupą.
Dla wygody przyjmuje się następujące oznaczenia:

Podalgebry
Algebra  jest podalgebrą algebry
jest podalgebrą algebry  , jeśli
, jeśli
 oraz
oraz  .
.
- Uwaga
Niech  będzie algebrą. Na to, aby
będzie algebrą. Na to, aby  było uniwersum podalgebry algebry
było uniwersum podalgebry algebry  potrzeba i wystarcza, aby
potrzeba i wystarcza, aby 
- Uwaga
Niech  będzie algebrą i niech
będzie algebrą i niech  . Wówczas wśród podalgebr algebry
. Wówczas wśród podalgebr algebry  , których uniwersum zawiera
, których uniwersum zawiera  istnieje algebra najmniejsza.
istnieje algebra najmniejsza.
Algebrę tę nazywamy podalgebrą wyznaczoną przez  i oznacza się
i oznacza się ![\mathcal{A}[C]](http://upload.wikimedia.org/math/c/0/e/c0e9798f9d1ff8d8229a7e173a86157a.png) albo
albo  .
.
Przykłady
- Algebra
 jest podalgebrą algebry
jest podalgebrą algebry 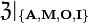 .
. - Podalgebrą algebry
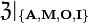 generowaną przez
generowaną przez  jest
jest 
- Podalgebrą algebry
 generowaną przez
generowaną przez  jest
jest 
- Uniwersum podalgebry algebry
 generowanej przez
generowanej przez  jest
jest 
- Podalgebrą algebry
 generowanej przez
generowanej przez  jest
jest 
Homomorfizmy
Niech  i
i  będą algebrami tej samej sygnatury
będą algebrami tej samej sygnatury  .
.
Funkcję  jest homomorfizmem algebr
jest homomorfizmem algebr  i
i  , jeśli
, jeśli

Rodzinę wszystkich homomorfizmów z  do
do  oznaczamy
oznaczamy  .
.
Homomorfizm różnowartościowy nazywamy monomorfizmem. Rodzinę wszystkich monomorfizmów z  do
do  oznaczamy
oznaczamy  .
.
Homomorfizm "na" nazywamy epimorfizmem. Rodzinę wszystkich epoimorfizmów z  do
do  oznaczamy
oznaczamy  .
.
Różnowartościowy epimorfizm, to izomorfizm. Rodzinę wszystkich izomorfizmów z  do
do  oznaczamy
oznaczamy  .
.
Homomorfizmy algebry w siebie, to endomorfizmy. Izomorfizmy w siebie, to automorfizmy.
Rodzinę wszystkich endomorfizmów algebry  oznaczamy
oznaczamy  . Rodzinę wszystkich automorfizmów algebry
. Rodzinę wszystkich automorfizmów algebry  oznaczamy
oznaczamy  .
.
Rodzina automorfizmów algebry w siebie tworzy z działaniem
składania
odwzorowań
grupę
.
Zauważmy, że algebra  jest podalgebrą algebry
jest podalgebrą algebry  wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy  .
.
Jeśli  , to podalgebrę algebry
, to podalgebrę algebry  wyznaczoną przez
wyznaczoną przez 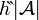 nazywamy obrazem homomorfizmu h i oznaczamy
nazywamy obrazem homomorfizmu h i oznaczamy  .
.
Przykłady
- Odwzorowanie
 jest w
jest w 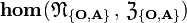 ,
,
ale nie jest ani w  , ani w
, ani w  .
. - Odwzorowanie
 jest w
jest w  , ale nie jest w
, ale nie jest w  .
. - Jedynym homomorfizmem
 w
w  jest
jest  .
. - Jedynymi homomorfizmami
 w
w  są
są  i
i  .
. - Jedynym homomorfizmem
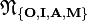 w
w  jest
jest  .
. - Jedynymi homomorfizmami
 i
i  są postaci
są postaci  , dla pewnego
, dla pewnego 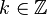 .
.
Kongruencje, zasadnicze twierdzenie algebry
Niech  będzie algebrą sygnatury
będzie algebrą sygnatury  .
.
Relacja równoważności
 w
w 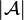 jest kongruencją algebry, gdy
jest kongruencją algebry, gdy
 ,
,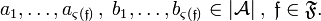
Przykład
Niech  i niech
i niech

Wówczas  jest kongruencją algebry
jest kongruencją algebry  .
.
Algebra ilorazowa
Niech  będzie algebrą sygnatury
będzie algebrą sygnatury  i niech
i niech  będzie kongruencją w
będzie kongruencją w  .
.
Algebrą ilorazową  przez
przez  jest algebra
jest algebra  , której uniwersum jest zbiór ilorazowy
, której uniwersum jest zbiór ilorazowy  i w której:
i w której:

Przyporządkowanie  nazywamy odwzorowaniem kanonicznym i oznaczamy je symbolem
nazywamy odwzorowaniem kanonicznym i oznaczamy je symbolem  . Jest ono homomorfizmem algebr
. Jest ono homomorfizmem algebr  i
i  .
.
Zasadnicze twierdzenie algebry
Niech  , wówczas
, wówczas  i
i  są izomorficzne.
są izomorficzne.
Szczególne algebry
W poniższej sekcji opisano ważne z punktu widzenia matematyki algebry ogólne.
Zbiór
Zbiór to algebra  sygnatury
sygnatury 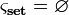 .
.
Jest to przypadek zdegenerowany, z punktu widzenia algebry – nieistotny.
Zbiór z wyróżnionym punktem
Zbiór z wyróżnionym punktem to algebra  sygnatury
sygnatury  , gdzie element
, gdzie element  nazywa się elementem bądź punktem wyróżnionym algebry
nazywa się elementem bądź punktem wyróżnionym algebry  .
.
Element ten oznacza się niekiedy symbolem  . Zazwyczaj jednak element wyróżniony oznacza się małą literą, która służy do oznaczania uniwersum algebry (czasem z indeksem dolnym 0).
. Zazwyczaj jednak element wyróżniony oznacza się małą literą, która służy do oznaczania uniwersum algebry (czasem z indeksem dolnym 0).
Algebra unarna
Algebra unarna to algebra 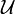 sygnatury
sygnatury  , gdzie
, gdzie  może mieć wiele różnych oznaczeń w zależności od zastosowań, np.
może mieć wiele różnych oznaczeń w zależności od zastosowań, np.  ,
, 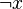 , czy − x w
notacji prefiksowej
, x', x − 1 w
notacji postfiksowej
, czy też
, czy − x w
notacji prefiksowej
, x', x − 1 w
notacji postfiksowej
, czy też  z wykorzystaniem
znaków diakrytycznych
.
z wykorzystaniem
znaków diakrytycznych
.
Grupoid
Grupoid to algebra 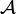 sygnatury
sygnatury  , czyli inaczej mówiąc zbiór z
działaniem dwuargumentowym
.
, czyli inaczej mówiąc zbiór z
działaniem dwuargumentowym
.
Zamiast  zwykle pisze się
zwykle pisze się  lub nawet xy (tzw. notacja multyplikatywna) lub x + y (tzw. notacja addytywna), gdzie
lub nawet xy (tzw. notacja multyplikatywna) lub x + y (tzw. notacja addytywna), gdzie  .
.
W notacji multyplikatywnej działanie grupoidu nazywa się mnożeniem, a w notacji addytywnej – dodawaniem. Notacja addytywna używana jest zazwyczaj, gdy działanie grupoidu jest
przemienne
.
Quasi-grupa
Quasi-grupa to
wzbogacenie
grupoidu 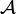 do sygnatury
do sygnatury  , w którym spełnione są równości:
, w którym spełnione są równości:
 ,
,
gdzie
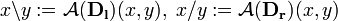 , gdzie
, gdzie  .
.
Działania „ / ” i „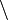 ” nazywa się odpowiednio dzieleniem prawo- i lewostronnym.
” nazywa się odpowiednio dzieleniem prawo- i lewostronnym.
Lupa
Lupa (pętla) to wzbogacenie quasigrupy 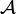 do sygnatury
do sygnatury  , które spełnia równości
, które spełnia równości
 ,
,
gdzie  .
.
Innymi słowy, pętla to quasigrupa z
elementem neutralnym
mnożenia.
Półgrupa
Półgrupa to grupoid z działaniem
łącznym
.
Monoid
Monoid to wzbogacenie półgrupy 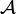 do sygnatury
do sygnatury  , które spełnia równości
, które spełnia równości
 ,
,
gdzie  w notacji multyplikatywnej, często też
w notacji multyplikatywnej, często też  . W notacji addytywnej zamiast
. W notacji addytywnej zamiast  pisze się zwykle 0.
pisze się zwykle 0.
Monoid można określić jako półgrupę z elementem neutralnym działania tej półgrupy.
Grupa
Grupa jest wzbogaceniem monoidu 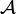 do sygnatury
do sygnatury  , które spełnia równości
, które spełnia równości
 dla
dla  .
.
Standardowym oznaczeniem  jest x − 1, niekiedy również
jest x − 1, niekiedy również  , w notacji multyplikatywnej; element ten nazywa się wtedy elementem odwrotnym do x. W notacji addytywnej element ten oznacza się symbolem − x i nazywa elementem przeciwnym do x.
, w notacji multyplikatywnej; element ten nazywa się wtedy elementem odwrotnym do x. W notacji addytywnej element ten oznacza się symbolem − x i nazywa elementem przeciwnym do x.
Grupa to, innymi słowy, monoid z operacją brania
elementu odwrotnego/przeciwnego
.
Pierścień
Pierścień to algebra 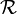 sygnatury
sygnatury  , dla której
redukt
, dla której
redukt
 jest
grupą przemienną
, a
jest
grupą przemienną
, a  jest półgrupą oraz spełnione są równości:
jest półgrupą oraz spełnione są równości:
 i
i  dla
dla  ,
,
gdzie
 ,
,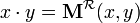 ,
, ,
,
dla  .
.
Działanie  nazywamy dodawaniem pierścienia, a działanie
nazywamy dodawaniem pierścienia, a działanie  jego mnożeniem.
jego mnożeniem.
- Uwaga
- W dowolnym pierścieniu zachodzi
 .
. - Ponieważ
 , to
, to  . Podobnie
. Podobnie  .
.
Pierścień, w którym działanie  jest przemienne nazywa się pierścieniem przemiennym.
jest przemienne nazywa się pierścieniem przemiennym.
Pierścień z jedynką
Pierścień z jedynką to algebra 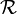 sygnatury
sygnatury  , że
, że 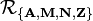 jest pierścieniem, a
jest pierścieniem, a  jest monoidem.
jest monoidem.
Element  nazywamy jedynką pierścienia
nazywamy jedynką pierścienia 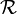 . Oznaczamy go zazwyczaj symbolem 1.
. Oznaczamy go zazwyczaj symbolem 1.
Pierścień z dzieleniem
Pierścień z dzieleniem to algebra 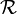 sygnatury
sygnatury  , że
, że  jest pierścieniem, a
jest pierścieniem, a  jest grupą.
jest grupą.
Dla wygody przyjmuje się oznaczenie:
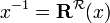 , gdzie
, gdzie  .
.
Ciało
Ciało to pierścień z dzieleniem z
przemiennym
działaniem mnożenia.
Krata
Kratą nazywamy algebrę  sygnatury
sygnatury  , w której spełnione są równości:
, w której spełnione są równości:
 ,
,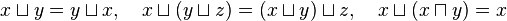 ,
,
gdzie użyto oznaczeń

oraz
 .
.
Krata rozdzielna to krata spełniająca co najmniej jedną z równości (pozostała równość wynika z przyjętej):

bądź
 .
.
Innym warunkiem, tak koniecznym jak i dostatecznym, na rozdzielność kraty jest zachodzenie równości:
 , gdzie
, gdzie  .
.
Krata jest nierozdzielna, gdy zawiera podkratę izomorficzną z jedną z poniższych krat:
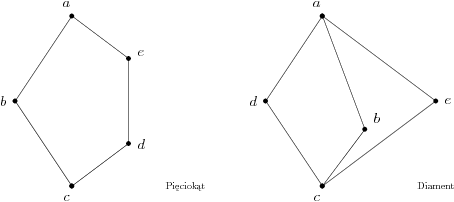 |
Minimalne kraty nierozdzielne |
Należy jednak być przezornym, niżej zaprezentowane kraty są rozdzielne:
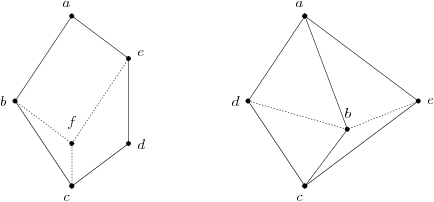 |
To są kraty rozdzielne, mimo iż wydaje się, że zawierają wymienione wyżej kraty |
Krata dualna
Redukt  jest także kratą. Kratę tę nazywamy kratą dualną do
jest także kratą. Kratę tę nazywamy kratą dualną do  . Krata dualna do kraty rozdzielnej jest kratą rozdzielną.
. Krata dualna do kraty rozdzielnej jest kratą rozdzielną.
Krata z „zerem”
Krata z „zerem” to wzbogacenie kraty  do sygnatury
do sygnatury  , w której spełnione są równości:
, w której spełnione są równości:
 oraz
oraz  ,
,
gdzie element  nazywa się spodem lub zerem kraty
nazywa się spodem lub zerem kraty  .
.
Krata z „jedynką”
Krata z „jedynką” to wzbogacenie kraty  do sygnatury
do sygnatury 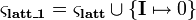 , w której spełnione są równości:
, w której spełnione są równości:
 oraz
oraz  ,
,
gdzie element  nazywa się szczytem lub jedynką kraty
nazywa się szczytem lub jedynką kraty  .
.
Krata ograniczona
Krata ograniczona to wzbogacenie kraty  do sygnatury
do sygnatury  , że
, że  jest kratą z zerem, a
jest kratą z zerem, a  jest kratą z jedynką.
jest kratą z jedynką.
Krata komplementarna
Krata komplementarna to wzbogacenie kraty ograniczonej do sygnatury  , w której spełnione są równości:
, w której spełnione są równości:
 oraz
oraz  ,
,
gdzie  nazywa się uzupełnieniem elementu x w
nazywa się uzupełnieniem elementu x w  .
.
Komplementarną kratę rozdzielną nazywa się algebrą Boole'a.
Redukt  jest także algebrą Boole'a. Algebrę tę nazywamy dualizacją algebry
jest także algebrą Boole'a. Algebrę tę nazywamy dualizacją algebry  .
.
Krata implikacyjna
Relacja  zdefiniowana wzorem
zdefiniowana wzorem
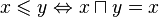
definiuje w każdej kracie
porządek
zwany porządkiem kratowym, w którym operacje  i
i  są tożsame z operacjami
infimum i supremum
. Równoważnie porządek ten można zadać wzorem
są tożsame z operacjami
infimum i supremum
. Równoważnie porządek ten można zadać wzorem
 .
.
Krata implikacyjna to wzbogacenie kraty  do sygnatury
do sygnatury  , w której zachodzi:
, w której zachodzi:
 ,
,
gdzie element 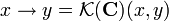 nosi nazwę relatywnego pseudouzupełnienia elementu x względem y.
nosi nazwę relatywnego pseudouzupełnienia elementu x względem y.
W kracie implikacyjnej zachodzi m.in. związek:
 dla dowolnego
dla dowolnego  .
.
Każda krata implikacyjna jest rozdzielna.
Algebra Heytinga
Algebra Heytinga to wzbogacenie kraty implikacyjnej  do sygnatury
do sygnatury  , której redukt
, której redukt  jest kratą z zerem i w której zachodzi równość:
jest kratą z zerem i w której zachodzi równość:
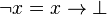 ,
,
gdzie 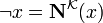 dla
dla  .
.
- Uwaga
- Algebra Heytinga zazwyczaj nie jest wzbogaceniem algebry Boole'a:
 |
Przykład algebry Heytinga, która nie jest algebrą Boole'a |
Algebra Łukasiewicza
- Ta sekcja jest . Jeśli możesz, .
Zobacz też