Algorytm Euklidesa –
algorytm
znajdowania
największego wspólnego dzielnika
(NWD) dwóch
liczb naturalnych
. Nie wymaga
rozkładania
liczb na
czynniki pierwsze
. Algorytm wymyślił
Eudoksos z Knidos
(
IV wiek p.n.e.
), a
Euklides
jedynie zawarł go w swoim dziele
Elementy
.
W algorytmie wykorzystywana jest zależność
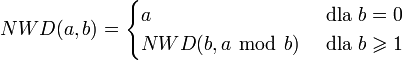
Algorytm
Przebieg algorytmu Euklidesa obliczania NWD liczb a i b:
- oblicz c jako resztę z dzielenia a przez b
- zastąp pozycję a liczbą b, a pozycję b liczbą c
- jeżeli pozycja b = 0, to szukane NWD = a, w przeciwnym wypadku przejdź do 1
Zapis w
pseudokodzie
:
NWD(liczba całkowita a, liczba całkowita b) dopóki b != 0 c := reszta z dzielenia a przez b a := b b := c zwróć a
Zapis w
C++
:
int NWD (int a, int b){ int c; while (b != 0) { c = a % b; a = b; b = c; } return a;}Zapis w
Pascalu
:
function nwd(a,b:integer):integer; begin while a<>b do if a>b then a:=a-b else b:=b-a; nwd:=a; end;
Przykłady
Największy wspólny dzielnik


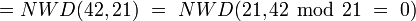 .
.
Stąd

Względna pierwszość
Jeżeli największym wspólnym dzielnikiem dwóch liczb jest 1, to są one
względnie pierwsze
. Przykład dla 46406 i 36957:
| a | b |
|---|
| 46406 | 36957 |
| 36957 | 9449 |
| 9449 | 8610 |
| 8610 | 839 |
| 839 | 220 |
| 220 | 179 |
| 179 | 41 |
| 41 | 15 |
| 15 | 11 |
| 11 | 4 |
| 4 | 3 |
| 3 | 1 |
| 1 | 0 |
Dowód poprawności
Lemat: 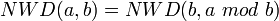
- Aby to wykazać, należy udowodnić, że wspólny podzielnik liczb a i b jest również podzielnikiem liczby

- Przyjmijmy:
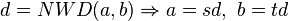

- gdzie
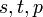 są liczbami całkowitymi.
są liczbami całkowitymi.
- Wtedy:

- zatem
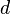 jest również podzielnikiem
jest również podzielnikiem 
Z lematu wynika przez
indukcję
, że jeśli algorytm się zakończy, to da poprawny wynik. Pozostaje udowodnić, że się zakończy. Wystarczy w tym celu zauważyć, że 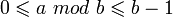 , więc w każdym kroku algorytmu wartość
, więc w każdym kroku algorytmu wartość 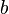 zmniejsza się przynajmniej o 1. Ponieważ nie może nigdy być ujemna, algorytm musi się zakończyć.
zmniejsza się przynajmniej o 1. Ponieważ nie może nigdy być ujemna, algorytm musi się zakończyć.
Złożoność czasowa
Dla dowolnych liczb 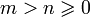 algorytm Euklidesa zwraca wartość NWD(m, n) po co najwyżej
algorytm Euklidesa zwraca wartość NWD(m, n) po co najwyżej 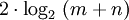 przebiegach pętli.
przebiegach pętli.
Dowód
- Lemat: Jeśli
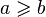 to
to
- (1) jest równoważne
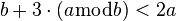
- Podstawiając
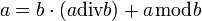
- otrzymuje się:
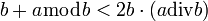
- i ponieważ
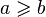 to
to  , oraz ponadto z własności
modulo
, oraz ponadto z własności
modulo
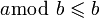 otrzymujemy:
otrzymujemy: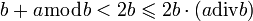
- Przy pierwszej iteracji mamy
 , po k-tym przebiegu pętli:
, po k-tym przebiegu pętli:
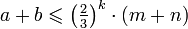
- Ponieważ
 , po ostatnim, l-tym przebiegu pętli będzie:
, po ostatnim, l-tym przebiegu pętli będzie:
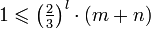

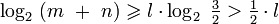

Największej liczby kroków algorytmu wymagają dwa kolejne elementy
ciągu Fibonacciego
.
Rozszerzony algorytm Euklidesa
Jeśli przechowywana będzie informacja o kolejnych ilorazach, to będzie też można wyznaczyć
liczby całkowite
w równaniu  . Ta metoda nazywana jest rozszerzonym algorytmem Euklidesa.
. Ta metoda nazywana jest rozszerzonym algorytmem Euklidesa.
Na przykład dla liczb 174 i 18 w algorytmie Euklidesa uzyskuje się wyniki pośrednie:

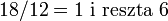
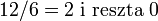
lub przepisując wszystkie równania w taki sposób, by w pierwszym równaniu po prawej stronie występowała tylko suma pewnych wielokrotności liczb 174 i 18:

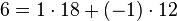
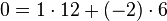
Zauważmy, że w pierwszym równaniu po prawej stronie występuje kombinacja liniowa liczb 174 i 18, podobnie jak w równaniu  . W następnych równaniach po prawej stronie mamy zawsze kombinację liniową liczb 174, 18 lub liczb, które wystąpiły po lewej stronie we wcześniejszych równaniach.
. W następnych równaniach po prawej stronie mamy zawsze kombinację liniową liczb 174, 18 lub liczb, które wystąpiły po lewej stronie we wcześniejszych równaniach.
Kluczowa dla rozszerzonego algorytmu Euklidesa staje się możliwość stopniowego zastępowania tych liczb przez kombinacje liniowe liczb wejściowych aż do otrzymania równości:

np.

Zapis algorytmu w pseudokodzie:
// Zakładamy, że a > 0 i b > 0.a0 = ab0 = b// Inicjalizacja. Utrzymujemy niezmienniki p*a0 + q*b0 = a oraz r*a0 + s*b0 = bp = 1; q = 0;r = 0; s = 1;// algorytmwhile (b != 0) c = a mod b quot = floor( a/b ) a = b b = c new_r = p - quot * r new_s = q - quot * s p = r; q = s r = new_r s = new_s// Wówczas NWD(a0, b0) = p*a0 + q*b0
Zobacz też
Linki zewnętrzne