Cyrkulacja operator wprowadzony początkowo w
dynamice płynów
następnie uogólniony na wszystkie
pola wektorowe
, dla danego pola definiuje wielkość
skalarną
. Cyrkulacja oznaczana jest zwyczajowo przez 
.
Dla przepływającego płynu z prędkością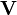 
wzdłuż zamkniętej krzywej C cyrkulacja określona jest wzorem:
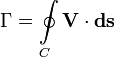
gdzie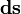 
oznacza wektor styczny do krzywej całkowania.
Niezerowa wartość cyrkulacji oznacza, że w analizowanym obszarze występuje zawirowanie cieczy, przy wartości dodatniej w kierunku zgodnym z przyjętym kierunkiem całkowania.
Według
twierdzenia Kutty-Żukowskiego
w przepływie laminarnym cyrkulacja
płynu
(powietrza) wokół ciała poruszającego się w nim jest jednakowa dla każdej krzywej całkowania, a wytwarzana
siła nośna
jest proporcjonalna do cyrkulacji.
Definicja uogólniona
Cyrkulacja dla danego pola wektorowego 
wzdłuż krzywej L określa wzór:
gdzie:
jest infinitezymalnym wektorem stycznym do krzywej w danym punkcie.
Jeżeli krzywa L ma parametryzację 
w przedziale ![t \in [a,b]](http://upload.wikimedia.org/math/c/9/e/c9ef8c742260828c469822e9c5dbe2c9.png)
, to powyższy wzór można zapisać jako:
Związek cyrkulacji z rotacją
Twierdzenie Stokesa
wiąże całkę po krzywej zamkniętej ze
strumieniem
rotacji
przenikającym przez powierzchnię zamkniętą tą krzywą.
Ze związku powyższego wynika:
Równanie to oznacza, że dla danej krzywej L ograniczającej pewną powierzchnię S, która jest uznana za płask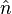ą, 
- jest
wersorem
(wektor o długości 1) prostopadłym (normalnym) do tej powierzchni, iloczyn skalarny rotacji i wersora normalnego w wybranym punkcie pola jest równy granicy do której dąży iloraz cyrkulacji po krzywej zamkniętej otaczającej jeden raz wybrany punkt przez powierzchnię ograniczoną tą krzywą.
