Iloczyn skalarny – operator na przestrzeni liniowej przypisujący dwóm argumentom z tej przestrzeni rzeczywistą wartość skalarną . Czasami spotyka się również nazwę iloczyn wewnętrzny, jednak odnosi się ono zwykle do ogólniejszych iloczynów skalarnych w przestrzeniach unitarnych .

Artykuł ten opisuje domyślny iloczyn skalarny ortonormalnych przestrzeni euklidesowych nazywany (dla odróżnienia od innych możliwych) zwykłym, standardowym bądź euklidesowym; niżej określenia te będą pomijane.

Definicja i przykłady

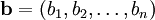Iloczyn skalarny dwóch wektorów (z rozważanej przestrzeni euklidesowej) oraz wynosi z definicji

.

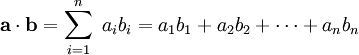Przykładowo iloczyn skalarny dwóch trójwymiarowych wektorów (1,3, − 5) oraz (4, − 2, − 1) jest równy

.

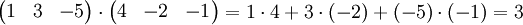Korzystając z mnożenia macierzy i traktując wektory (kolumnowe) jako macierze wymiaru , iloczyn skalarny można także zapisać jako

,

gdzie oznacza transpozycję macierzy .

W powyższym przykładzie uzyskamy wówczas mnożenie -macierzy (np. wektora) przez -wektor (który ze względu na naturę mnożenia macierzy da w wyniku -macierz, np. skalar):

.

Interpretacja geometryczna

|a|•cos(θ) jest rzutem skalarnym a na b

W przestrzeni euklidesowej istnieje silna zależność między iloczynem skalarnym a długością i kątem . Dla wektora , jest kwadratem jego długości, a ogólniej, jeśli jest innym wektorem, to

,

gdzie

oznaczają długość (wartość) oraz ,

θ jest kątem między nimi.

Ponieważ jest rzutem skalarnym na , iloczyn skalarny może być rozumiany geometrycznie jako iloczyn tego rzutu przez długość .

Ponieważ cosinus wynosi zero, to iloczyn skalarny dwóch prostopadłych wektorów jest zawsze równy zeru. Jeżeli oraz mają długość jeden (są wersorami ), to iloczyn skalarny daje w wyniku po prostu kosinus kąta między nimi. Dlatego, dla danych dwóch wektorów, kąt między nimi może być wyznaczony przez przekształcenie powyższego wzoru:

.

Czasem własności te służą jako definicja iloczynu skalarnego, szczególnie w dwóch lub trzech wymiarach. Oczywiście definicja ta jest równoważna powyższej. Dla wyższych wymiarów wzór ten może być użyty do zdefiniowania pojęcia kąta.

Własności geometryczne uzależnione są od bazy wektorów prostopadłych o jednostkowej długości. Można przyjąć takiej bazy lub użyć dowolnej bazy i zdefiniować długość oraz kąt (włączając w to prostopadłość) jak wyżej.

Jak pokazuje interpretacja geometryczna, iloczyn skalarny jest niezmienniczy ze względu na izometryczne zmiany bazy: obroty, odbicia oraz kombinacje przy zachowaniu początku.

Innymi słowy i ogólniej dla dowolnego n iloczyn skalarny jest niezmienniczy ze względu na zmianę współrzędnych obrazowaną macierzą ortogonalną . Odpowiada to następującym dwóm warunkom:

• nowa baza jest także ortonormalna (tzn. jest ortonormalna w stosunku do poprzedniej),
• nowe wektory bazy mają taką samą długość jak stare (tzn. jednostkowe, jeżeli są wyrażone wektorami starej bazy)

Fizyka

W fizyce iloczyn skalarny jest w powszechnym użyciu, co wynika bezpośrednio z faktu, że zarówno w fizyce klasycznej jak i kwantowej podstawę matematyczną badań stanowią przestrzenie liniowe z określonym na niej iloczynem skalarnym, przykładami mogą być:

• trójwymiarowa przestrzeń euklidesowa ,
• przestrzeń Hilberta w mechanice kwantowej .

W zależności od dziedziny fizyki oraz kontekstu korzysta się z różnych sposobów zapisu iloczynu skalarnego

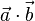• , gdzie są wektorami ;
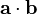• , gdzie są wektorami .

Iloczyn skalarny ( iloczyn wewnętrzny ) bywa też oznaczany

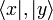, gdzie są wektorami w przestrzeni Hilberta (zob. notacja Diraca ).

Przykładem wielkości fizycznej definiowanej za pomocą iloczynu skalarnego jest praca mechaniczna , która jest iloczynem skalarnym siły i przemieszczenia .

Własności

Następujące własności są prawdziwe dla dowolnych wektorów oraz dowolnego skalara r:

• przemienność :

  ,

• rozdzielność względem dodawania:

  ,

• dwuliniowość :

  .

Przy mnożeniu przez wartość skalarną zachodzi następująca równość:

.

Ostatnie dwie własności wynikają z dwóch pierwszych.

Dwa niezerowe wektory oraz są prostopadłe wtedy i tylko wtedy, gdy .

Jeżeli jest wektorem jednostkowym , to iloczyn skalarny określa wartość rzutu w kierunku , ze znakiem ujemnym, jeżeli kierunek jest przeciwny. Często przydatne jest rozkładanie wektorów w celu ich wygodnego dodawania, np. obliczania siły wypadkowej w mechanice .

W przeciwieństwie do mnożenia liczb, gdzie jeżeli , to o ile to , dla iloczynu skalarnego nie zachodzi prawo skracania. Jeżeli , to korzystając z prawa rozdzielności możemy zapisać równoważną równość . Jest ona spełniona, gdy czynniki są ortogonalne , czyli zachodzi dowolna kombinacja warunków:

• pierwszy wektor jest zerowy: , lub
• drugi wektor jest zerowy: , czyli , lub
• wektory są prostopadłe : .

Spełnienie trzeciego warunku prowadzi więc do spełnienia równości , nawet gdy i .

Reprezentacja macierzowa

Iloczyn wewnętrzny może być przedstawiony w formie macierzy. Niech dane będą dwa wektory

wyrażone w bazie S,

.

wówczas każdy iloczyn wewnętrzny może być przedstawiony następująco:

,

gdzie jest reprezentacją -macierzową iloczynu wewnętrznego. Dla danej macierzy iloczynu wewnętrznego w bazie 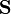oznaczanej , macierz może być obliczona przez rozwiązanie następującego układu równań :

Przykład

Dany jest zbiór bazowy

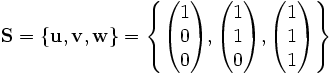
oraz macierz iloczynu wewnętrznego wyrażonego w ,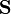

.

Możemy przyrównać każdy element C_S do iloczynu skalarnego dwóch wektorów bazowych wg wzoru

.

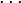Tym sposobem otrzymujemy dziewięć równań i tyleż niewiadomych. Ich rozwiązanie daje

Uogólnienia

Iloczyn skalarny uogólnia się na abstrakcyjne przestrzenie liniowe nazywane wtedy przestrzeniami unitarnymi , wówczas oznacza się go zwykle . Ze względu na interpretację geometryczną iloczynu skalarnego norma wektora w takiej przestrzeni unitarnej zdefiniowana jest jako

tak, że uogólnia długość oraz kąt θ między dwoma wektorami oraz przez

.

Iloczyn wewnętrzny Frobeniusa określa iloczyn wewnętrzny na macierzach, jak gdyby były one wektorami dwuwymiarowymi, sumując iloczyny odpowiadających sobie elementów.

Dowód interpretacji geometrycznej

Uwaga 

Ten dowód przeprowadzony jest dla wektorów trójwymiarowych, ale łatwo uogólnia się na wektory n-wymiarowe.

Niech będzie dany wektor

.

Kilkakrotne zastosowanie twierdzenia Pitagorasa daje względem jego długości v równość

.

Jest to jednak to samo, co

,

a więc iloczyn wektora przez siebie to kwadrat jego długości.

Lemat 1

.

Niech wektory oraz będą zaczepione w początku układu i skierowane do siebie pod kątem θ. Trzeci wektor może być zdefiniowany jako

,

tworząc przy tym trójkąt o bokach a,b,c. Zgodnie z twierdzeniem cosinusów mamy

.

Podstawiając iloczyny skalarne za podniesione do kwadratu długości, zgodnie z lematem 1, otrzymuje się

(1)

Ponieważ , jest również

,

co, zgodnie z prawem rozdzielności, rozszerza się do

(2)

Łącząc obydwa równania , (1) oraz (2), dostaje się

.

Odjęcie od obu stron i podzielenie przez − 2 daje ostatecznie

.

Zobacz też

• iloczyn wektorowy
• mnożenie macierzy
• nierówność Cauchy'ego-Schwarza

Linki zewnętrzne

• Demonstracja iloczynu skalarnego wykonana w Javie
• Inna demonstracja iloczynu skalarnego w Javie
• Wytłumaczenie iloczynu skalarnego dla wektorów zespolonych