Iloczyn wektorowy - działanie przyporządkowujące parze
wektorów
 wektor γ taki, że
wektor γ taki, że
Iloczyn wektorowy wektorów α i β oznaczany jest symbolem 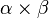 .
.
Sposób obliczania
Mając
definicję
iloczynu mieszanego
skonstruowaną za pomocą iloczynu wektorowego i
skalarnego
, można przedstawić iloczyn wektorowy jako macierz wersorów
układu kartezjańskiego
wraz ze współrzędnymi dwóch wektorów, dzięki któremu wyznaczamy iloczyn wektorowy. Zapiszmy iloczyn skalarny wektora  przez iloczyn wektorowy wektorów
przez iloczyn wektorowy wektorów 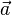 i
i  w następujący sposób:
w następujący sposób:
Wektor 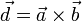 jest prostopadły do wektorów
jest prostopadły do wektorów 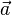 oraz do
oraz do  i tym samym układ wektorów
i tym samym układ wektorów 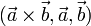 tworzy nową bazę o wymiarze trzy zanurzoną w starej bazie w układzie kartezjańskim o takim samym wymiarze.
tworzy nową bazę o wymiarze trzy zanurzoną w starej bazie w układzie kartezjańskim o takim samym wymiarze.
W definicji iloczynu mieszanego (1) wprowadziliśmy parametr η=±1, ponieważ z definicji wspomnianego iloczynu mieszanego z na razie z niewyznaczonym parametrem wynika, że iloczyn wektorowy jest prostopadły do wektorów, z którego on jest wyznaczony. Istnieją dwa rodzaje tych wektorów, różniące się tylko zwrotami i dlatego w tej definicji występuje ten wspomniany parametr, by określić te dwa wektory. Parametr η wyznaczymy poniżej, a więc wybierzemy jeden z dwóch tych wektorów, tak by definicja iloczynu wektorowego była taka, by zbudowana na podstawie niej baza określająca nowy układ współrzędnych w oparciu o te trzy wspomniane wcześniej wektory (dwa wektory na podstawie, której jest zbudowany nasz iloczyn wektorowy i trzeci wektor, który jest wynikiem rozważanego tego iloczynu), była taka by skrętność tego nowego układu współrzędnych była zgodna ze starym układem współrzędnym, w którym współrzędne tych trzech wektorów są wyznaczone.
Niech baza starego układu odniesienia posiadała
bazę kanoniczną
. Z definicji iloczynu skalarnego możemy zatem wyznaczyć współrzędne wyniku iloczynu wektorowego, którego przedstawienie matematyczne na razie bliżej nie znany, ale chcemy wyznaczyć w prostokątnym układzie współrzędnym względem określonego wektora bazy kanonicznej. To możemy tak zrobić wykorzystując definicję iloczynu mieszanego jako iloczyn pewnego wektora (w tym przypadku są wektory bazy starego układu współrzędnych) i iloczynu wektorowego dwóch dowolnych wektorów.
Zatem wyznaczmy jego współrzędne iloczynu wektorowego względem pierwszego wektora
bazy kanonicznej
w starym układzie współrzędnych  . wtedy mamy:
. wtedy mamy:
Następnie wyznaczmy jego współrzędne iloczynu wektorowego względem drugiego wektora
bazy kanonicznej
w starym układzie współrzędnych  . wtedy mamy:
. wtedy mamy:
wyznaczmy jego współrzędne iloczynu wektorowego względem trzeciego wektora
bazy kanonicznej
układu współrzędnych  . wtedy mamy:
. wtedy mamy:
Jeśli weźmiemy  , to układ trzech wektorów
, to układ trzech wektorów  jako nowy układ współrzędnych jest zgodny ze starym układem współrzędnym kartezjańskim, gdy
wyznacznik
macierzy przejścia
ze starego układu współrzędnych no nowego spełnia warunek det(T) > 0. Zbudujmy macierz przejścia.
jako nowy układ współrzędnych jest zgodny ze starym układem współrzędnym kartezjańskim, gdy
wyznacznik
macierzy przejścia
ze starego układu współrzędnych no nowego spełnia warunek det(T) > 0. Zbudujmy macierz przejścia.
Wykorzystując definicję wektora  , które współrzędne są podane w punktach (2), (3) i (4), uzyskujemy wyznacznik macierzy T (5), którego zapis matematyczny wygląda następująco:
, które współrzędne są podane w punktach (2), (3) i (4), uzyskujemy wyznacznik macierzy T (5), którego zapis matematyczny wygląda następująco:
Aby w naszej nowej bazie skrętność była zgodna ze skrętnością starego układu trójwymiarowego kartezjańskiego, musi zachodzić η = 1 wedle obliczeń (6).
Udowodniliśmy więc, że iloczyn wektorowy dwóch dowolnych wektorów jest dany tak, by jego definicja na podstawie wcześniejszych rozważa i η = 1 (obliczenia (6)) była napisana następująco;
Podwójny iloczyn wektorowy
Poniżej udowodniony zostanie wzór nazywany wzorem na podwójny iloczyn wektorowy:  spełniony dla dowolnych
spełniony dla dowolnych  , czyli wektorów
, czyli wektorów  będących elementami przestrzeni trójwymiarowej.
będących elementami przestrzeni trójwymiarowej.
Dowód
Dowód przeprowadzony będzie w oparciu o definicję iloczynu wektorowego i iloczynu skalarnego za pomocą współrzędnych wektorów wchodzących w skład podwójnego iloczynu wektorowego. Skorzystamy tu z nieformalnej
definicji iloczynu wektorowego w przestrzeni trójwymiarowej
jako macierzy, w której występują
ortonormalne
wersory
.
Co kończy dowód.
Własności
- Iloczyn dwóch takich samych wektorów jest wektorem zerowym, ponieważ są one liniowo zależne w trywialny sposób.
- Iloczyn wektorowy jest
antyprzemienny
(w szczególności nie jest
przemienny
). Dokładniej: iloczyn wektorowy zmienia zwrot po zamianie kolejności dowolnych dwóch argumentów:
 .
. - Iloczyn wektorowy nie jest łączny, ale
 (w przestrzeni 3-wymiarowej).
(w przestrzeni 3-wymiarowej). - Iloczyn wektorowy danych wektorów nie zmieni się, jeśli do danego pierwszego wektora dodamy dowolną wielokrotność drugiego danego wektora lub odwrotnie,np:
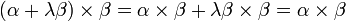
Jeżeli weźmiemy dwa wektory, tzn. ![\alpha=[a_x,\,a_y,\,a_z]](http://upload.wikimedia.org/math/8/d/a/8daefbd45018046a89243f93373e0c94.png) i
i ![\beta =[b_x,\,b_y,\,b_z]](http://upload.wikimedia.org/math/3/a/f/3aff2af3d54c1fab8088bafb1aa430b0.png) , to ich iloczyn wektorowy można wyliczyć przy pomocy następującego wzoru mnemotechnicznego (nie jest on formalnie poprawny ponieważ elementami
macierzy
nie mogą być jednocześnie
liczby
i wektory):
, to ich iloczyn wektorowy można wyliczyć przy pomocy następującego wzoru mnemotechnicznego (nie jest on formalnie poprawny ponieważ elementami
macierzy
nie mogą być jednocześnie
liczby
i wektory):
![\alpha \times \beta =\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\a_x&a_y&a_z\\b_x&b_y&b_z\end{vmatrix}=[a_yb_z-a_zb_y, \,-a_xb_z+a_zb_x, \,a_xb_y-a_yb_x]](http://upload.wikimedia.org/math/8/5/3/853ff3198a52f94f11be405c5f37900a.png)
- długość wektora wynikowego jest równa iloczynowi wartości obu wektorów wyjściowych pomnożonego przez
sinus
kąta
między nimi zawartego:
 ,
,
Wektor normalny a prostopadłość
Dane są 3 wektory:



Zakładamy, że wektory  i
i  są prostopadłe do wektora
są prostopadłe do wektora  . Wynika więc stąd, że pomiędzy wektorem
. Wynika więc stąd, że pomiędzy wektorem  a
a  oraz pomiędzy
oraz pomiędzy  a
a 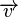 nawiązuje się
relacja
prostopadłości
:
nawiązuje się
relacja
prostopadłości
:

Ponieważ jest to układ dwóch
równań
z trzema
niewiadomymi
, potraktujemy niewiadomą 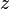 jako pewną daną, zaś wyrazy
jako pewną daną, zaś wyrazy  i
i  - jako
wyrazy wolne
, po czym przeniesiemy je na drugą stronę powyższych równań, zmieniając przy tym oczywiście ich
znaki
na przeciwne:
- jako
wyrazy wolne
, po czym przeniesiemy je na drugą stronę powyższych równań, zmieniając przy tym oczywiście ich
znaki
na przeciwne:

Następnie, korzystając ze
wzorów Cramera
, wyznaczamy wartości niewiadomych  i
i  , w zależności od wartości niewiadomej
, w zależności od wartości niewiadomej 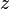 :
:



Powołując się na jedną z własności wyznacznika, z  i
i  możemy wyciągnąć przed nawias wyrażenie
możemy wyciągnąć przed nawias wyrażenie  :
:


Powołując się na kolejną własność wyznacznika, w  możemy zamienić miejscami kolumny, zmieniając przy tym znak na przeciwny:
możemy zamienić miejscami kolumny, zmieniając przy tym znak na przeciwny:
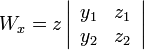
Na końcu otrzymujemy:

Zauważmy, że wyrażenia  i
i  mają wspólny mianownik równy
mają wspólny mianownik równy  . Załóżmy więc, że:
. Załóżmy więc, że:

Wówczas wyrażenia  ,
,  i
i 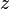 przedstawiają się następująco:
przedstawiają się następująco:

Ostatecznie, otrzymaliśmy składowe wektora normalnego 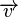 , będącego iloczynem wektorowym wektorów
, będącego iloczynem wektorowym wektorów  i
i  , tak więc prawdziwy jest wzór:
, tak więc prawdziwy jest wzór:

Uogólnienie - iloczyn wektorialny
Niech V będzie  -wymiarową
przestrzenią euklidesową
o zadanej
orientacji
. Iloczynem wektorowym
wektorów
-wymiarową
przestrzenią euklidesową
o zadanej
orientacji
. Iloczynem wektorowym
wektorów
 nazywamy wektor
nazywamy wektor  taki, że
taki, że
- Jeśli
 są
liniowo zależne
, to
są
liniowo zależne
, to  jest wektorem zerowym.
jest wektorem zerowym. - Jeśli
 są
liniowo niezależne
, to
są
liniowo niezależne
, to
Działanie to oznaczamy  lub
lub 
Interpretacja geometryczna
W przestrzeni  -wymiarowej, długość wektora otrzymanego jako iloczyn wektorowy danych n − 1 wektorów jest równa
objętości
równoległościanu
rozpiętego na tych wektorach (otrzymujemy wektor zerowy, gdy dane wektory są liniowo zależne). Ponadto wektor wynikowy jest prostopadły do wszystkich danych wektorów i jest zorientowany tak, że baza oparta na danych wektorach i wektorze wynikowym jest dodatnio zorientowana.
-wymiarowej, długość wektora otrzymanego jako iloczyn wektorowy danych n − 1 wektorów jest równa
objętości
równoległościanu
rozpiętego na tych wektorach (otrzymujemy wektor zerowy, gdy dane wektory są liniowo zależne). Ponadto wektor wynikowy jest prostopadły do wszystkich danych wektorów i jest zorientowany tak, że baza oparta na danych wektorach i wektorze wynikowym jest dodatnio zorientowana.
W przestrzeni trójwymiarowej, długość iloczynu wektorowego jest równa iloczynowi długości pierwszego wektora i długości rzutu drugiego wektora na kierunek prostopadły do pierwszego wektora, czyli polu
równoległoboku
na nich rozpiętego. Wektor zerowy otrzymamy, gdy jeden z danych wektorów jest zerowy lub gdy dane wektory są równoległe.
Bibliografia
- I.N. Bronsztejn: K.A.Siemiendiawjew Matematyka Poradnik encyklopedyczny - PWN Warszawa 1996
Zobacz też