Środek masy ciała lub układu ciał jest punktem , w którym skupiona jest cała masa w opisie układu jako masy punktowej . Pojęcie to jest wykorzystywane także w geometrii .

Wzór na wektor wodzący środka masy

Powyższa zależność dla ośrodków ciągłych, zapisana w postaci wyrażeń całkowych, wiąże środek masy z rozkładem gęstości ρ w przestrzeni za pomocą zależności:

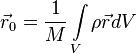
przy czym:

• to wektor wodzący środka masy;

• M – masa ciała;
• V – objętość ciała;
• ρ = ρ(x,y,z) – funkcja gęstości ciała.

Dla ciała znajdującego się w jednorodnym polu grawitacyjnym środek ciężkości pokrywa się ze środkiem masy.

Gdy ciało wiruje lub drga, istnieje w tym ciele punkt zwany środkiem masy, który porusza się w taki sam sposób, w jaki poruszałby się pojedynczy punkt materialny poddany tym samym siłom zewnętrznym.

Środek geometryczny

Obliczanie środka geometrycznego przebiega w podobny sposób jak obliczanie środka masy z tym, że nie występuje tu gęstość, więc ze wzoru na środek masy można uzyskać wzór na środek ciężkości przyjmując równość mas wszystkich elementów, stałą gęstość lub stałą gęstość powierzchniową czy liniową.

Położenie środka geometrycznego układu punktów określa wektor

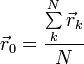
gdzie N – liczba elementów układu.

Położenie środka geometrycznego bryły jest dane wektorem

Możliwe jest także obliczanie środka geometrycznego powierzchni dwuwymiarowych lub krzywych w przestrzeni trójwymiarowej (zob. np. wielościan dualny ).

Położenie środka geometrycznego powierzchni jest zdefiniowane wektorem

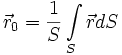
a dla krzywych

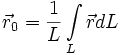
gdzie:

• S – pole powierzchni ,
• dS – element powierzchni,
• L – długość krzywej ,
• dL – element krzywej.

a całkowanie przebiega po całej powierzchni lub całej krzywej.

W sympleksie barycentrum pozwala zdefiniować m.in. układ współrzędnych barycentrycznych .

Zobacz też

• współrzędne barycentryczne
• antypodyzm
• środek ciężkości
• średnia ważona