|
PFA (aksjomat)
PFA (aksjomat)PFA (z
ang.
proper forcing axiom) - jeden z
aksjomatów
forsingowych
używanych w
teorii mnogości
,
topologii
i pokrewnych dziedzinach
matematyki
. Jest to zdanie postulujące szczególną własność pewnych
porządków częściowych
. Definicje Pojęcia wstępneNiech  będzie
pojęciem forsingu
. będzie
pojęciem forsingu
. - Powiemy, że zbiór
 jest
filtrem
w jest
filtrem
w  jeśli następujące warunki są spełnione: jeśli następujące warunki są spełnione:
- (i)
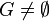 , , - (ii) jeśli
 , , 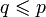 oraz oraz 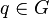 , to również , to również  , , - (iii) jeśli
 , to można znaleźć , to można znaleźć 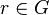 taki że taki że 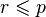 oraz oraz  . .
dla każdego  , jeśli r,q są niesprzeczne, to , jeśli r,q są niesprzeczne, to  - (Przypomnijmy, że warunki r,q są niesprzeczne jeśli istnieje warunek
 silniejszy niż oba te warunki.) silniejszy niż oba te warunki.)
- Pojęcie forsingu
 jest
proper
, jeśli dla każdej dostatecznie dużej regularnej liczby kardynalnej χ istnieje jest
proper
, jeśli dla każdej dostatecznie dużej regularnej liczby kardynalnej χ istnieje 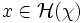 taki, że: taki, że:
- jeśli N jest przeliczalnym elementarnym podmodelem
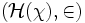 , ,  oraz oraz 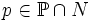 , , - to istnieje warunek
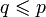 który jest który jest 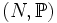 -generyczny. -generyczny.
PFA i BPFAPFA oznacza następujące zdanie: - jeśli pojęcie forsingu
 jest proper, jest proper,  jest rodziną gęstych podzbiorów jest rodziną gęstych podzbiorów  oraz oraz  , , - to istnieje filtr
 który ma niepusty przekrój z każdym zbiorem z który ma niepusty przekrój z każdym zbiorem z  (tzn (tzn 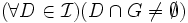 ). ).
BPFA jest następującym zdaniem: - jeśli pojęcie forsingu
 jest proper, jest proper,  jest rodziną maksymalnych antyłańcuchów w zupełnej
algebrze Boole'a jest rodziną maksymalnych antyłańcuchów w zupełnej
algebrze Boole'a
 wyznaczonej przez to pojęcie forsingu oraz zarówno wyznaczonej przez to pojęcie forsingu oraz zarówno  jak i każdy antyłańcuch w rodzinie jak i każdy antyłańcuch w rodzinie  jest mocy co najwyżej jest mocy co najwyżej  , , - to istnieje filtr
 który ma niepusty przekrój z każdym antyłańcuchem z który ma niepusty przekrój z każdym antyłańcuchem z  (tzn (tzn 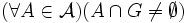 ). ).
Nazwa BPFA jest skrótem angielskiego zwrotu Bounded Proper Forcing Axiom. Historia i niesprzeczność- Idea forsingów proper i związanego z nimi aksjomatu forsingowego była stworzona przez
izraelskiego
matematyka
Saharona Shelaha
w drugiej połowie
lat 70. XX wieku
. W
1978
w czasie wykładów w
Berkeley
przedstawił on po raz pierwszy ten koncept, w druku ukazał się on w
1980
[1].
- W
1982
, Shelah opublikował
monografię
[2] przedstawiającą pierwsze sytematyczne badania forsingów proper, związanych z nimi aksjomatów forsingowych i twierdzeń zachowawczych.
- W
1995
, Martin Goldstern i Saharon Shelah wprowadzają BPFA[3] który zyskał sporą popularność w ostatnich latach (ze względu na słabsze założenia potrzebne aby wykazać jego niesprzeczność).
Podstawą do wykazania niesprzeczności PFA (czy też BPFA) jest twierdzenie Shelaha mówiące, że iteracja z przeliczalnym nośnikiem forsingów proper jest forsingiem proper (a więc nie kolapsuje ω1)[4][5][6] Niestety, w iteracjach tego typu liczby kardynalne powyżej  mogą być kolapsowane, jeśli więc chcemy przeiterować wszystkie możliwe forsingi proper to potrzebujemy dodatkowego narzędzia aby złapać swój własny ogon. Narzędziem tym jest zwykle diament Lavera związany z liczbą super-zwartą. mogą być kolapsowane, jeśli więc chcemy przeiterować wszystkie możliwe forsingi proper to potrzebujemy dodatkowego narzędzia aby złapać swój własny ogon. Narzędziem tym jest zwykle diament Lavera związany z liczbą super-zwartą. - Twierdzenie [Shelah]: Jeśli teoria "ZFC+istnieje
liczba super-zwarta
" jest niesprzeczna, to również teoria "ZFC+PFA" jest niesprzeczna.
Aksjomat BPFA wymaga znacznie słabszych założeń: - Twierdzenie [Goldstern-Shelah]: Jeśli teoria "ZFC+istnieje
liczba Mahlo
" jest niesprzeczna, to również teoria "ZFC+BPFA" jest niesprzeczna.
(W tym ostatnim twierdzeniu trochę mniej niż istnienie liczby Mahlo jest wymagane; co więcej Goldstern i Shelah podali dokładną siłę niesprzeczności BPFA.) Przykłady forsingów proper- Wszystkie przeliczalnie domknięte pojęcia forsingu jak też i wszystkie ccc pojęcia forsingu są proper.
- Pojęcia forsingu Lavera, Mathiasa i Sacksa (zdefiniowane w artykule o
pojęciach forsingu
) są proper.
- Pojęcia forsingu zbudowane zgodnie z metodą norm na możliwościach są proper przy naturalnych warunkach[7].
Przykłady konsekwencjiZałóżmy PFA. Wówczas: Aby przedstawić kolejną konsekwencję PFA musimy wprowadzić następującą definicję. Powiemy, że podzbiór 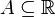 prostej rzeczywistej
jest
prostej rzeczywistej
jest  -gęsty w -gęsty w 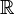 jeśli dla każdego niepustego
przedziału otwartego jeśli dla każdego niepustego
przedziału otwartego
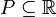 mamy, że mamy, że  . . - Zakładając PFA, każde dwa
 -gęste podzbiory prostej są porządkowo
izomorficzne
[8]. -gęste podzbiory prostej są porządkowo
izomorficzne
[8].
Bibliografia- ↑ Shelah, Saharon: Independence results. "J. Symbolic Logic" 45 (1980), s. 563-573.
- ↑ Shelah, Saharon: Proper forcing. "Lecture Notes in Mathematics", 940. Springer-Verlag, Berlin-New York, 1982. .
- ↑ Goldstern, Martin; Shelah, Saharon: The bounded proper forcing axiom. "J. Symbolic Logic" 60 (1995), s. 58-73.
- ↑ Shelah, Saharon: Proper and improper forcing. "Perspectives in Mathematical Logic". Springer-Verlag, Berlin, 1998. .
- ↑ Goldstern, Martin: Tools for your forcing construction. Set theory of the reals (Ramat Gan, 1991). "Israel Math. Conf. Proc.", 6, Bar-Ilan Univ., Ramat Gan, 1993, s. 305-360.
- ↑ Abraham, Uri: Proper forcing. w: Handbook of Set Theory pod red. M. Foremana, A. Kanamoriego i M. Magidora, w druku. Dostępne w formacie
dvi
na
stronie autora
.
- ↑ Rosłanowski, Andrzej; Shelah, Saharon: Norms on possibilities. I. Forcing with trees and creatures. "Mem. Amer. Math. Soc." 141 (1999), no. 671, .
- ↑ Baumgartner, James: Applications of the proper forcing axiom, w: Handbook of set-theoretic topology, s. 913-959. North-Holland, Amsterdam, 1984.
Zobacz też
Inne hasła zawierające informacje o "PFA (aksjomat)":
Ewolucja
...
Analiza czynnikowa
...
Bertrand Russell
...
PFA
PFA (aksjomat)
polioksymetylen
...
PFA (aksjomat)
...
Aksjomat Martina
...
Diagram Cichonia
...
Diament Jensena
...
Pojęcie forsingu
...
Filtr (matematyka)
...
Inne lekcje zawierające informacje o "PFA (aksjomat)":
21. Myśl polityczna. Liberalizm (plansza 12)
...
|