Proces stochastyczny - rodzina zmiennych losowych określonych na pewnej przestrzeni probabilistycznej o wartościach w pewnej przestrzeni mierzalnej. Najprostszym przykładem procesu stochastycznego jest wielokrotny rzut monetą: dziedziną funkcji jest zbiór liczb naturalnych (liczba rzutów), natomiast wartością funkcji dla danej liczby jest jeden z dwóch możliwych stanów losowania (zdarzenie), orzeł lub reszka. Nie należy mylić procesu losowego, którego wartości są zdarzeniami losowymi, z funkcją, która zdarzeniom przypisuje wartość prawdopodobieństwa ich wystąpienia (mamy wówczas do czynienia z rozkładem gęstości prawdopodobieństwa).

W praktyce dziedziną , na której zdefiniowana jest funkcja, jest najczęściej przedział czasowy (taki proces stochastyczny nazywany jest szeregiem czasowym ) lub obszar przestrzeni (wtedy nazywany jest polem losowym). Jako przykłady szeregów czasowych można podać: fluktuacje giełdowe , sygnały, takie jak mowa , dźwięk i wideo , dane medyczne takie jak EKG i EEG , ciśnienie krwi i temperatura ciała, losowe ruchy takie jak ruchy Browna . Przykładami pól losowych są statyczne obrazy, losowe krajobrazy i układ składników w niejednorodnych materiałach.

Definicja

Niech T będzie niepustym zbiorem, który będziemy dalej nazywać zbiorem indeksów, 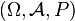będzie przestrzenią probabilistyczną oraz będzie przestrzenią mierzalną. Rodzinę zmiennych losowych

,

to znaczy rodzinę funkcji -mierzalnych nazywamy procesem stochastycznym. Przestrzeń nazywamy przestrzenią fazową albo przestrzenią stanów procesu X.

Często za zbiór T przyjmuje się przedział 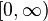lub zbiór liczb naturalnych , za E zbiór liczb rzeczywistych , a za rodzinę , to znaczy rodzinę borelowskich podzbiorów prostej.

Procesy stochastyczne, których zbiór indeksów jest przeliczalny nazywamy łańcuchami (zob. łańcuch Markowa ).

Związek z wielowymiarową zmienną losową

Oczywiście matematyczna definicja funkcji dopuszcza przypadek "funkcja ze zbioru {1,...,n} w R jest wektorem w Rⁿ", więc wielowymiarowa zmienna losowa ma tę samą definicję, co proces stochastyczny. W praktyce jednak odróżnia się te terminy, rezerwując nazwę "proces stochastyczny" dla modeli zjawisk rozciągających się w czasie, gdzie każdy z elementów wektora opisuje jedną chwilę lub przedział czasowy. O wielowymiarowej zmiennej losowej mówi się natomiast częściej wtedy, gdy wszystkie elementy wektora opisują różne parametry w tej samej chwili czasowej.

Interesujące przypadki specjalne

• procesy Bernoulliego
• proces Wienera
• procesy Markowa to takie, w których przyszłość jest warunkowo niezależna od przeszłości przy danej teraźniejszości.
• procesy Poissona
• procesy stacjonarne
• procesy homogeniczne: proces, gdzie dziedzina posiada pewną symetrię i skończenie-wymiarowe rozkłady prawdopodobieństwa także mają tę symetrię. Specjalny przypadek obejmuje proces stacjonarny .
• procesy o przyrostach niezależnych : procesy, gdzie dziedzina jest przynajmniej częściowo uporządkowana i jeśli x₁ <...< x_n, wszystkie zmienne f(x_k+1) − f(x_k) są niezależne
• procesy punktowe: losowe ustawienia punktów w przestrzeni S
• procesy gaussowskie : procesy, gdzie wszystkie liniowe kombinacje współrzędnych są zmiennymi losowymi z rozkładem normalnym
• martyngały
• procesy Galtona-Watsona
• proces gałązkowy
• ruchy Browna

Przykłady

• błądzenie losowe

Procesy stacjonarne

Proces stochastyczny X(t) nazywamy procesem stacjonarnym (w wąskim sensie) jeżeli dla każdego (t₁,t₂,...t_n) łączny rozkład {X(t₁ + t₀),X(t₂ + t₀),...X(t_n + t₀)} nie zależy od t₀. Innymi słowy, właściwości takiego procesu nie zmieniają się przy przesunięciu osi czasu.

Proces stochastyczny X(t) nazywamy procesem stacjonarnym w szerszym sensie, jeżeli:

1. 
2. EX(t) = μ jest stałe
3. E{(X(t) − μ)(X(s) − μ)} zależy tylko od różnicy t-s

Źródło definicji: Eugene Wong: Procesy stochastyczne w teorii informacji i układach dynamicznych. Warszawa: WNT, 1971. 

Konstruowanie procesów stochastycznych

W normalnej aksjomatyzacji teorii prawdopodobieństwa środkami teorii miary , podstawowym zadaniem jest konstrukcja sigma-algebry zbiorów mierzalnych w przestrzeni wszystkich funkcji i zbudowanie na niej skończonej miary . W tym celu tradycyjnie używa się metody zwanej rozszerzeniem Kołmogorowa.

Rozszerzenie Kołmogorowa

Rozszerzenie Kołmogorowa przebiega według następującego schematu: zakładając, że miara prawdopodobieństwa na przestrzeni wszystkich funkcji f : X → Y istnieje, może być ona użyta do zdefiniowania rozkładu prawdopodobieństwa dla skończenie-wymiarowych zmiennych losowych [f(x₁),...,f(x_n)]. Teraz, z tego n-wymiarowego rozkładu prawdopodobieństwa możemy uzyskać (n-1)-wymiarowe rozkład brzegowy dla [f(x₁),...,f(x_n-1)]. Istnieje oczywisty warunek zastosowania metody, mianowicie taki, że ten rozkład brzegowy musi być taki sam jak ten uzyskany z w pełni rozwiniętego procesu stochastycznego. Kiedy wyrazimy ten warunek w kategoriach gęstości rozkładów , rezultatem będzie równanie Chapmana-Kołmogorowa-Smoluchowskiego.

Twierdzenie o rozszerzeniu Kołmogorowa gwarantuje istnienie procesu stochastycznego z daną rodziną skończenie-wymiarowych rozkładów prawdopodobieństwa spełniających warunek Chapmana-Kołmogorowa.

Czego rozszerzenie Kołmogorowa nie obejmuje

W aksjomatyzacji Kołmogorowa, zbiory mierzalne są zbiorami, które mają prawdopodobieństwo, innymi słowy, zbiorami dla których pytania tak/nie mają probabilistyczną odpowiedź.

Rozszerzenie Kołmogorowa zaczyna się deklaracją, że mierzalne są wszystkie zbiory funkcji, gdzie skończenie wiele współrzędnych [f(x₁),...,f(x_n)] leży w mierzalnych podzbiorach Yⁿ. Innymi słowy, jeśli na pytania tak/nie o f można uzyskać odpowiedź biorąc co najwyżej skończoną liczbę współrzędnych, wtedy pytanie ma probabilistyczną odpowiedź.

W teorii miary, jeśli mamy przeliczalną rodzinę mierzalnych zbiorów, wtedy suma i przecięcia wszystkich tych zbiorów jest zbiorem mierzalnym. Dla naszych celów oznacza to, że te pytania tak/nie, które zależą od policzalnie wielu współrzędnych, mają probabilistyczną odpowiedź.

Rozszerzenie Kołmogorowa umożliwia konstruowanie procesów stochastycznych z ustalonymi skończenie-wymiarowymi rozkładami. Każde pytanie, które można zadać na temat ciągu, ma także probabilistyczną odpowiedź dla ciągów losowych. Z drugiej strony, pewne pytania o funkcje określone na ciągłej dziedzinie nie mają probabilistycznej odpowiedzi. Niestety większość problemów analizy matematycznej należy do tej kategorii, w szczególności:

1. ograniczoność
2. ciągłość
3. różniczkowalność

wszystkie wymagają znajomości niepoliczalnie wielu wartości funkcji.

Jednym z rozwiązań jest zdefiniowanie procesu stochastycznego jako rozkładalnego. Innymi słowy, że istnieje policzalny zbiór współrzędnych {f(x_i)} którego wartości definiują całą funkcję losową f.

Zobacz też

• wektor losowy
• szereg czasowy
• teoria prawdopodobieństwa