Sortowanie przez scalanie

W informatyce sortowanie przez scalanie ( ang. merge sort), to rekurencyjny algorytm sortowania danych, mający zastosowanie przy danych dostępnych sekwencyjnie (po kolei, jeden element na raz), na przykład w postaci listy jednokierunkowej (tj. łączonej jednostronnie) albo pliku sekwencyjnego . Odkrycie algorytmu przypisuje się Johnowi von Neumannowi .

Algorytm

Algorytm ten jest dobrym przykładem algorytmów typu Dziel i zwyciężaj ( ang. divide and conquer), których ideą działania jest podział problemu na mniejsze części, których rozwiązanie jest już łatwiejsze.

Wyróżnić można trzy podstawowe kroki:

1. Podziel zestaw danych na dwie, równe części (w przypadku nieparzystej liczby wyrazów jedna część będzie o 1 wyraz dłuższa);
2. Zastosuj sortowanie przez scalanie dla każdej z nich oddzielnie, chyba że pozostał już tylko jeden element;
3. Połącz posortowane podciągi w jeden.

Procedura scalania dwóch ciągów A[1..n] i B[1..m] do ciągu C[1..m+n]:

1. Utwórz wskaźniki na początki ciągów A i B → i=1, j=1
2. Jeżeli ciąg A wyczerpany (i>n), dołącz pozostałe elementy ciągu B do C i zakończ pracę.
3. Jeżeli ciąg B wyczerpany (j>m), dołącz pozostałe elementy ciągu A do C i zakończ pracę.
4. Jeżeli A[i] ≤ B[j] dołącz A[i] do C i zwiększ i o jeden, w przeciwnym przypadku dołącz B[j] do C i zwiększ j o jeden
5. Powtarzaj od kroku 2 aż wszystkie wyrazy A i B trafią do C

Scalenie wymaga O(n+m) operacji porównań elementów i wstawienia ich do tablicy wynikowej.

Złożoność czasowa

Sortowanie przez scalanie zastosowane do tablicy 7-elementowej.

Bez straty ogólności załóżmy, że długość ciągu, który mamy posortować jest potęgą liczby 2 (patrz Złożoność obliczeniowa )

Obrazek obok przedstawia drzewo rekursji wywołania algorytmu mergesort.

Mamy więc drzewo o głębokości log₂ n, na każdym poziomie dokonujemy scalenia o łącznym koszcie n×c, gdzie c jest stałą zależną od komputera. A więc intuicyjnie, tzn. nieformalnie możemy dowieść, że złożoność algorytmu mergesort to log₂ n×n

Formalnie złożoność czasową sortowania przez scalanie możemy przedstawić następująco:

T(1) = O(1)

Ciągi jednoelementowe możemy posortować w czasie stałym, czas sortowania ciągu n–elementowego to scalenie dwóch ciągów –elementowych, czyli O(n), plus czas potrzebny na posortowanie dwóch o połowę krótszych ciągów.

Mamy:

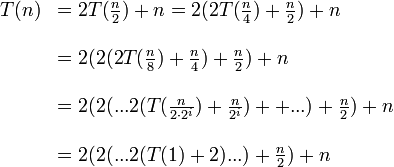
gdzie n = 2^k

Po rozwinięciu nawiasów otrzymamy:

T(n) = 2nlogn

A więc asymptotyczny czas sortowania przez scalanie wynosi O(n log n) (zobacz: notacja dużego O ).

Dowód poprawności algorytmu

Dowód przez indukcję względem długości n tablicy elementów do posortowania.

1) n=2

Algorytm podzieli dane wejściowe na dwie części, po czym zastosuje dla nich scalanie do posortowanej tablicy

2) Zał.: dla ciągów długości k, k<n algorytm mergesort prawidłowo sortuje owe ciągi.

Dla ciągu długości n algorytm podzieli ten ciąg na dwa ciągi długości n/2. Na mocy założenia indukcyjnego ciągi te zostaną prawidłowo podzielone i scalone do dwóch posortowanych ciągów długości n/2. Ciągi te zostaną natomiast scalone przez procedurę scalającą do jednego, posortowanego ciągu długości n.

Pseudokod

Struktura tablica jest tablicą, której elementy mogą być zmieniane, argumenty start, koniec są całkowitoliczbowe.

procedure merge(tablica, start, środek, koniec); var tab_pom : array [0..koniec-start] of integer;    i,j,k   : integer; begin   i := start;  k := 0;  j := środek + 1;   while (i <= środek) and (j <= koniec)     begin       if tablica[j] < tablica[i] then        begin           tab_pom[k] := tab[j];          j := j + 1;        end      else        begin          tab_pom[k] := tab[i]          i := i + 1;        end;      k := k + 1;    end;   if (i <= środek)    while (i <= środek)      begin        tab_pom[k] := tab[i];        i := i + 1;        k := k + 1;      end    else      while (j <= koniec)        begin          tab_pom[k] := tab[j];          j := j + 1;          k := k + 1;        end;   for i:= 0 to koniec-start do    tab[start + i] := tab_pom[i];   end;   procedure merge_sort(tablica, start, koniec); var środek : integer; begin   if start <> koniec then  begin     środek := (start + koniec) div 2;     merge_sort(tablica, start, środek);     merge_sort(tablica, środek + 1, koniec);     merge     (tablica, start, środek, koniec);  end; end;

Wersja nierekurencyjna

Podstawową wersję algorytmu sortowania przez scalanie można uprościć. Pomysł polega na odwróceniu procesu scalania serii. Ciąg danych możemy wstępnie podzielić na n serii długości 1, scalić je tak, by otrzymać serii długości 2, scalić je otrzymując 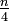, serii długości 4...

Złożoność obliczeniowa jest taka sama jak w przypadku klasycznym, tu jednak nie korzystamy z rekursji , a więc zaoszczędzamy czas i pamięć potrzebną na jej obsłużenie.

Linki zewnętrzne

• Przyśpieszony MergeSort