Fraktal

Fraktal ( łac. fractus – złamany, cząstkowy) w znaczeniu potocznym oznacza zwykle obiekt samo-podobny (tzn. taki, którego części są podobne do całości) albo "nieskończenie subtelny" (ukazujący subtelne detale nawet w wielokrotnym powiększeniu). Ze względu na olbrzymią różnorodność przykładów matematycy obecnie unikają podawania ścisłej definicji i proponują określać fraktal jako zbiór, który:

• ma nietrywialną strukturę w każdej skali,
• struktura ta nie daje się łatwo opisać w języku tradycyjnej geometrii euklidesowej,
• jest samo-podobny, jeśli nie w sensie dokładnym, to przybliżonym lub stochastycznym ,
• jego wymiar Hausdorffa jest większy niż jego wymiar topologiczny ,
• ma względnie prostą definicję rekurencyjną,
• ma naturalny ("poszarpany", "kłębiasty" itp.) wygląd.

Dokładniej, fraktalem nazwiemy zbiór, który posiada wszystkie te charakterystyki albo przynajmniej ich większość (zob. Falconer (1997)). Na przykład linia prosta na płaszczyźnie jest formalnie samo-podobna, ale brak jej pozostałych cech i zwyczajowo nie uważa się jej za fraktal. Z drugiej strony, zbiór Mandelbrota ma wymiar Hausdorffa równy 2, taki sam jak jego wymiar topologiczny. Jednak pozostałe cechy wskazują, że jest to fraktal.

Historia

Pojęcie fraktala zostało wprowadzone do matematyki przez francuskiego informatyka i matematyka polskiego pochodzenia Benoita Mandelbrota w latach siedemdziesiątych XX wieku . Odkryty przez niego zbiór Mandelbrota nie był jednak pierwszym przykładem fraktala. Wcześniej istniała już cała gama zbiorów o niecałkowitym wymiarze Hausdorffa , postrzeganych jednak głównie jako kontrprzykłady pewnych twierdzeń. Bardziej systematycznie fraktalami zajmowała się geometryczna teoria miary, mająca swoje początki w pracach Constantina Caratheodory'ego i Felixa Hausdorffa .

Szczególnymi fraktalami – nie nazywając ich po imieniu – zajmowali się Georg Cantor , Giuseppe Peano , Wacław Sierpiński , Paul Lévy , a także Donald Knuth . Szczególny wkład w rozwój geometrycznej teorii miary wniósł Abram Samoilovitch Besicovitch , który skonstruował również wiele konkretnych fraktali o paradoksalnych własnościach. Również zbiór Julii , ściśle związany ze zbiorem Mandelbrota , był badany w latach 20. zeszłego wieku . Mandelbrot używając komputera do wizualizacji uczynił z fraktali przedmiot intensywnych badań. O ważności tego zagadnienia zadecydowały zastosowania w różnych dziedzinach, zwłaszcza poza matematyką, np. obecnie prawie każdy telefon komórkowy korzysta z wbudowanej anteny fraktalnej . Liczne odpowiedniki fraktali istnieją też w naturze .

Własności

Za jedną z cech charakterystycznych fraktala uważa się samopodobieństwo, to znaczy podobieństwo fraktala do jego części. Co więcej, zbiory fraktalne mogą być samoafiniczne, tj. część zbioru może być obrazem całości przez pewne przekształcenie afiniczne . Dla figur samopodobnych można określić wielkość zwaną wymiarem samopodobieństwa lub wymiarem pudełkowym . Są to wielkości będące uogólnieniem klasycznych definicji wymiaru.

Wiadomo, że stosunek pól płaskich (wymiaru 2) figur podobnych równa się kwadratowi skali ich podobieństwa. Na przykład figura podobna do innej w skali 3 ma dziewięć razy większe pole od tamtej (9 = 3² albo 2 = log₃9). W przestrzeni stosunek objętości brył (trójwymiarowych) podobnych jest sześcianem skali ich podobieństwa; bryła podobna do innej w skali 2 ma osiem razy większą objętość od tamtej (8 = 2³ albo 3 = log₂8). Wymiar samopodobieństwa figury daje się zatem określić jako logarytm o podstawie równej skali podobieństwa i liczbie logarytmowej wskazującej, ile razy większa od figury wyjściowej (jaką częścią figury wyjściowej) jest figura podobna do niej w tej skali. Dla fraktali liczba ta może nie być całkowita.

Na przykład zbiór Cantora jest podobny do swoich dwu części w skali 3; wymiar Hausdorffa zbioru Cantora wynosi d = log 2/log 3=0,630929754... Analogicznie trójkąt Sierpińskiego jest podobny do swoich trzech części w skali 2, a jego wymiar Hausdorffa jest równy d = log 3/log 2 =1,584962501... Dywan Sierpińskiego jest podobny do swoich ośmiu części w skali 3, zatem jego wymiar Hausdorffa to d = log 8/log 3 =1,892789261...

Ogólniej, jeżeli fraktal składa się z N części, które łączą się między sobą na obszarze miary Lebesgue'a zero i są podobne w skali r do całego fraktala to wymiar Hausdorffa fraktala będzie równy log N/log r. Jeszcze ogólniej, jeśli założymy, że każda część jest podobna do całości w innej skali r_i, i=1,2,...,N, to wymiar Hausdorffa jest rozwiązaniem poniższego równania z niewiadomą s

Niektóre fraktale są zbiorami o mierze Lebesgue'a równej zero. Dotyczy to fraktali klasycznych, np. trójkąt Sierpińskiego i zbiór Cantora mają miarę Lebesgue'a równą zero. Ogólnie każdy fraktal dla którego wymiar Hausdorffa jest ostro większy od wymiaru topologicznego będzie mieć tę własność. Z kolei zbiór Mandelbrota i niektóre zbiory Julii mają dodatnie miary Lebesgue'a (na przykład miara Lebesgue'a zbioru Mandelbrota wynosi ok. 1,5).

Generowanie fraktali

Atraktory IFS

Najprostszą metodą tworzenia fraktali jest wykorzystanie zbioru przekształceń afinicznych będących przekształceniami zwężającymi (kontrakcjami). Transformując dowolny, niepusty zbiór zgodnie z regułą (tworząc ciąg zbiorów):

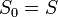
W granicy otrzymujemy:

,

atraktor układu, który w szczególności może być fraktalem. Zbiór nazywamy w tym przypadku systemem przekształceń iterowanych ( IFS ), zaś otrzymany w powyższej granicy fraktal jest atraktorem tego systemu. Jego istnienie wynika z twierdzenia Banacha o punkcie stałym odwzorowania zwężającego. W ten sposób można wygenerować m.in. następujące fraktale: zbiór Cantora , krzywa Kocha , smok Heighwaya , trójkąt Sierpińskiego , kostka Mengera , paproć Barnsleya .

W praktyce aby wygenerować fraktal wybieramy dowolny punkt x i transformujemy go kilka razy za każdym razem losując odpowiednio przekształcenie :

Procedurę tę powtarzamy np. kilka tysięcy razy. W szczególnych przypadkach dla efektu wizualnego może być istotny sposób losowania przekształceń. Np. dla paproci Barnsleya przekształcenia F_i, i=1..4 (zob. definicję ) losuje się z częstościami 85%, 7%, 7%, 1% odpowiednio.

Zbiory Julii i Mandelbrota

Zbiory takie jak zbiór Mandelbrota , zbiór Julii czy " płonący statek " są podzbiorami płaszczyzny zespolonej . Dla każdego punktu p określa się pewien ciąg z_n(p). Od zbieżności tego ciągu zależy czy punkt należy do zbioru (fraktala). Ciąg określa się wzorem rekurencyjnym :

Od postaci funkcji f i g zależy rodzaj fraktala.

Za punkty należące do danego zbioru uznaje się te, dla których:

Przykłady

• zbiór Mandelbrota :
• zbiór Julii zależy dodatkowo od ustalonego parametru c (dla każdego c otrzymujemy inny zbiór): .
• " płonący statek ": .

W praktyce liczenie ogranicza się do kilkudziesięciu iteracji lub do momentu gdy | z_n | > 2. Uzyskiwane kolory w obrazach fraktali (zwłaszcza zbiorów Julii) realizuje się np. zliczając, jak szybko poszczególne punkty rozbiegają się do nieskończoności i przydzielając im w zależności od tego różne barwy.

W przyrodzie

Struktury o budowie fraktalnej są powszechnie spotykane w przyrodzie. Przykładem mogą być krystaliczne dendryty (np. płatki śniegu), system naczyń krwionośnych, systemy wodne rzek, błyskawica lub kwiat kalafiora.

Przykłady

"Klasycznymi fraktalami", badanymi (czasem długo) przed powstaniem samego pojęcia fraktal, są m.in.:

• zbiór Cantora i związane z nim " diabelskie schody ",
• krzywe: funkcja Weierstrassa , krzywa Kocha , krzywa Peano , krzywa C Levy'ego,
• trójkąt Sierpińskiego , dywan Sierpińskiego , w oryginale opisane przez autora jako krzywe na płaszczyznie, fakt "niewidoczny" we współczesnych konstrukcjach. Uogólnienie "trójwymiarowe" dywanu to kostka Mengera ,
• smok Heighwaya ,
• zbiór Julii .

Inne ważne przykłady:

• fraktale otrzymywane w schemacie IFS (iterated function system), zob. niżej,
• bifurkacje Feigenbauma,
• dziwne atraktory w układach dynamicznych,
• fraktale Liapunowa,
• zbiór Mandelbrota .

Fraktale w matematyce

Zbiór Mandelbrota	Zbiór Mandelbrota - powiększony fragment	Zbiór Mandelbrota - kolejne powiększenie	Zbiór Mandelbrota - kolejne powiększenie
Kostka Mengera (IFS)	Atraktor IFS	Atraktor IFS	Paproć Barnsleya (Atraktor IFS)
Zbiór Julii w przestrzeni kwaternionów	Zbiór Julii	Siódma iteracja krzywej Kocha	Fraktal w przestrzeni trójwymiarowej
Etapy konstrukcji zbioru Cantora	Kostka Cantora	Krzywe smocze mogą wypełnić płaszczyznę	Krzywa C Levy'ego
4 etap konstrukcji krzywej Sierpińskiego

Fraktale w grafice komputerowej

Istnieje wiele programów dedykowanych do tworzenia obrazów fraktalnych, np. Fractint, Ultra Fractal, XenoDream, Tierazon, FractalExplorer, Apophysis, Sterling , QuaSZ, XaoS.

Fraktalopodobne obiekty w świecie rzeczywistym

Zdjęcie kalafiora Brassica oleracea	Zdjęcie wykonane teleskopem Hubble'a	Chmura	Chmury
Golfstrom	Fiordy Sognefjorden i Hardangerfjorden	Fiordy	Formacje skalne

Literatura

• Barnsley, Michael F., and Hawley Rising. Fractals Everywhere. Boston: Academic Press Professional, 1993.
• Falconer, Kenneth. Fractal Geometry: Mathematical Foundations and Applications. West Sussex: John Wiley & Sons, Ltd., 2003.
• Falconer, Kenneth. Techniques in Fractal Geometry. John Willey and Sons, 1997.
• Kudrewicz, Jacek. Fraktale i chaos. WNT.
• Mandelbrot, Benoît B. The Fractal Geometry of Nature. New York: W. H. Freeman and Co., 1982.

Zobacz też

• organizacja fraktalna (zarządzanie)
• Teoria ośrodków centralnych

Linki zewnętrzne

• Fraktale w katalogu DMOZ ( ang. )