Kwantyfikator – termin przyjęty w matematyce i logice matematycznej na oznaczenie zwrotów: dla każdego, istnieje takie i im pokrewnych, a także odpowiadającym im symbolom wiążacym zmienne w formułach . Są podstawowym elementem w rozwoju logiki pierwszego rzędu .

Kwantyfikatory odgrywają ważną rolę w formułowaniu twierdzeń i definicji matematycznych.

Kwantyfikator ogólny i szczegółowy

Zwrot dla każdego x nazywa się kwantyfikatorem ogólnym , kwantyfikatorem dużym lub kwantyfikatorem uniwersalnym wiążącym zmienną x. Kwantyfikator ogólny oznacza się symbolem lub , sporadycznie można spotkać również symbol (x) użyty w tym kontekście.

Zwrot istnieje takie x, że... uważa się za równoważny zwrotowi: dla pewnego x i nazywa się kwantyfikatorem szczegółowym, kwantyfikatorem małym lub kwantyfikatorem egzystencjalnym wiążącym zmienną x. Kwantyfikator szczegółowy oznacza się symbolem 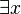lub , rzadziej także symbolem (Ex).

Stosowany jest także kwantyfikator a wypowiedź w tym przypadku brzmi " istnieje dokładnie jeden x". Formuły używające tego kwantyfikatora można zredukować do formuł odwołujących się tylko do . Np zdanie jest równoważne

.

Zmienne związane

Zmienna występująca pod znakiem kwantyfikatora nazywa się zmienną związaną danym kwantyfikatorem. Natomiast zmienna występująca w wyrażeniu matematycznym, która nie jest związana żadnym kwantyfikatorem, nazywa się zmienną wolną. Wyrażenie następujące po kwantyfikatorze, objęte tym kwantyfikatorem, nazywa się zasięgiem kwantyfikatora.

Jeżeli w zasięgu kwantyfikatora znajdują się jakieś inne kwantyfikatory, to kwantyfikator początkowy wiąże tylko te zmienne, które nie są związane żadnym kwantyfikatorem zawartym w jego zasięgu. Stosując kwantyfikator do formy zdaniowej , otrzymuje się nową formę zdaniową lub zdanie. Działanie to, zwane kwantyfikowaniem, jest funkcją jednoargumentową określoną w zbiorze form zdaniowych, której wartościami są zdania lub formy zdaniowe.

Kwantyfikatory przekształcają formy zdaniowe jednej zmiennej w zdania prawdziwe lub fałszywe. Kwantyfikując formę zdaniową mającą więcej niż jedną zmienną wolną, otrzymuje się nową formę zdaniową

Kwantyfikatory ograniczone

Czasami używa się kwantyfikatorów w których zmienna jest ograniczona do jakiegoś zbioru, np , . Kwantyfikatory te nazywane są kwantyfikatorami ograniczonymi i czyta się je dla każdego elementu x ze zbioru A mamy że, istnieje element x w zbiorze A taki, że. Kwantyfikatory te są skrótami następujących zapisów:

• to skrót na
• to skrót na .

Zbiór A powyżej bywa nazywany dziedziną lub uniwersum kwantyfikatora. Należy zwrócić uwagę, że jeśli uniwersum kwantyfikatora jest puste, to wartość logiczna otrzymanego zdania nie zależy od formuły P(x). I tak, dla każdej formuły P(x) (z jedną zmienną wolną x),

• jest zdaniem prawdziwym, a
• jest zdaniem fałszywym.

Aby przekonać się o słuszności powyższego stwierdzenia, wystarczy zauważyć iż pierwsze zdanie oznacza

.

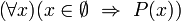Stwierdzenie "" jest zdaniem fałszywym (jakikolwiek wziąć x), zatem implikacja jest prawdziwa dla wszystkich x.

Rozważając zdanie "" zauważamy, że oznacza ono

.

Stwierdzenie "" jest zdaniem fałszywym (jakikolwiek wziąć x), zatem koniunkcja jest fałszywa dla wszystkich x.

Równoważnie, kwantyfikatory ograniczone można wprowadzić następująco.

• Zdanie "" oznacza, że ,
• zdanie "" oznacza, że .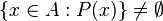

Jeśli 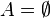, to oba zbiory i A są puste, a więc równe (bez względu na wybór formuły P(x). Czyli "" jest zawsze prawdziwe. Podobnie, "" jest fałszywe.

Przykłady

• Przypuśćmy, że rozważamy grupę ludzi (zbiór A). W tej grupie pewne osoby znają inne osoby i możemy wprowadzić relację Z(x,y) (na zbiorze A) wyrażającą stwierdzenie, że "osoba x zna osobę y". (Zauważmy, że z faktu iż x zna y wcale nie wynika, że y zna x – np y może być powszechnie znaną osobistościa.) Używając kwantyfikatorów możemy teraz wyrazić następujące obserwacje:

(a) osoba a zna każdą osobę w grupie:

(b) są ludzie którzy nie znają a:

(c) każdy zna każdego

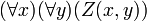
(d) pewna osoba nie zna nikogo (poza sobą samą):

.

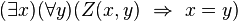W powyższych przykładach moglibyśmy użyć też kwantyfikatorów ograniczonych (pisząc itd), nie jest to jednak konieczne gdyż domniemana dziedzina realcji Z to właśnie zbiór A.

• Kolejność kwantyfikatorów może mieć znaczenie. Możemy zamienić kolejność kwantyfikatorów tego samego typu, np poniższe dwie formuły są równoważnymi sformułowaniami stwierdzenia, że funkcja jest ciągła :

• 
• .

Jednak zmieniając kolejność podkreślonej pary kwantyfikatorów 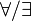otrzymamy definicję o wiele silniejszej własności, tzw. jednostajnej ciągłości :

.

• W formie zdaniowej , x jest zmienną związaną, zaś y zmienną wolną. Natomiast w wyrażeniu obie zmienne są związane.

Podstawowe własności logiczne

Niech R(x),S(x),T(x,y) będą formułami albo predykatami w pewnym języku. Następujące zdania są tautologiami logicznymi :

• ( Prawa De Morgana ),
• ,
• ,
• ,
• ,
• .

Inne kwantyfikatory

Wprowadzone powyżej kwantyfikatory nie są jedynymi spotykanymi w matematyce. Czasami rozważa się kwantyfikatory po predykatach (kwantyfikatory drugiego rzędu), kwantyfikatory po specjalnych obiektach czy też kwantyfikatory stwierdzające, że "istnieje dużo obiektów o pewnej własności" albo że "prawie wszystkie obiekty mają pewną własność".

W arytmetyce często używa się kwantyfikatorów ograniczonych, czyli takich, które przebiegają tylko pewne przedziały liczb zamiast wszystkich liczb. Wiele twierdzeń ze zwykłymi kwantyfikatorami da się przeformułować do postaci z kwantyfikatorami ograniczonymi, które są znacznie łatwiejsze do dowodzenia zarówno ręcznego jak i maszynowego.

Rozważa się także logiki inne niż klasyczna, np. logiki modalne lub logiki temporalne. W takich systemach istnieją dodatkowe kwantyfikatory wyrażające niestandardowe własności zmiennych.

Zobacz też

• skolemizacja
• forma preneksowa
• kwantyfikator Magidora-Malitza