Mechanika kwantowa

Zasada nieoznaczoności Heisenberga

Równanie Schrödingera Wstęp Aparat matematyczny Tło Mechanika klasyczna  · Stara teoria kwantów  · Interferencja  · Notacja Diraca  · Hamiltonian Koncepcje podstawowe Stan kwantowy  · Funkcja falowa  · Superpozycja  · Splątanie kwantowe  · Pomiar  · Nieoznaczoność  · Reguła Pauliego  · Dualizm korpuskularno-falowy  · Dekoherencja kwantowa  · Twierdzenie Ehrenfesta  · Tunelowanie Doświadczenia Doświadczenie Younga  · Doświadczenie Davissona-Germera  · Doświadczenie Sterna-Gerlacha  · Eksperymenty testujące twierdzenie Bella  · Doświadczenie Poppera  · Kot Schrödingera  · Problem testowania bomb Elitzura-Vaidmana  · Gumka kwantowa Sformułowania Obraz Schrödingera  · Obraz Heisenberga  · Obraz Diraca  · Mechanika macierzowa  · Suma po historiach Równania Równanie Schrödingera  · Równanie Pauliego  · Równanie Kleina-Gordona  · Równanie Diraca  · Wzór Rydberga Interpretacje de Broglie'a-Bohma  · Świadomość wywyołuje kolaps  · Spójne historie kwantowe  · Kopenhaska  · Statystyczna  · Zmiennych ukrytych  · Wielu światów  · Logika kwantowa  · Popularna  · Stochastyczna  · Transakcjonalna Zagadnienia zaawansowane Informatyka kwantowa  · Teoria rozpraszania  · Kwantowa teoria pola  · Chaos kwantowy Znani uczeni Planck  · Bohr  · Sommerfeld  · Bose  · Kramers  · Heisenberg  · Born  · Jordan  · Pauli  · Dirac  · de Broglie  · Schrödinger  · von Neumann  · Wigner  · Feynman  · Candlin  · Bohm  · Everett  · Bell  · Wien

Zjawisko tunelowe zwane też efektem tunelowym – zjawisko przejścia cząstki przez barierę potencjału o wysokości większej niż energia cząstki, opisane przez mechanikę kwantową . Z punktu widzenia fizyki klasycznej stanowi paradoks łamiący klasycznie rozumianą zasadę zachowania energii , gdyż cząstka przez pewien czas przebywa w obszarze zabronionym przez zasadę zachowania energii.

Zjawisko to zostało w 1928 roku zaproponowane przez Gamowa do wyjaśnienia rozpadu jąder. Wykorzystując zjawisko tunelowe Gamow dokonał obliczeń prowadzących do rezultatów zgodnych z doświadczeniem. Wkrótce obliczenia te zostały potwierdzone przez Condona i Gurneya, którzy uzyskali również rozwiązania dla przypadku syntezy jąder poprzez dołączanie nowych nukleonów. Born uogólnił efekt tunelowy na inne układy kwantowe, nie tylko te związane z potencjałem jądrowym.

Cząstka klasyczna w dole potencjału

Rozpatrzmy dla uproszczenia cząstkę o jednym stopniu swobody mogącą poruszać się tylko wzdłuż osi OX. Niech cząstka ta ma energię kinetyczną E_k i znajduje się w dole potencjału. Potencjał ten reprezentowany jest przez energię potencjalną cząstki E_p(x). Energia cząstki jest sumą energii kinetycznej i potencjalnej

Ponieważ energia kinetyczna jest nieujemna, klasyczna fizyka dopuszcza tylko ruch w obszarach gdzie

Zatem cząstka może przebywać w obszarach x₁ < x < x₂ oraz x > x₃, natomiast w obszarze x₂ < x < x₃ nie może się znaleźć, ponieważ jej energia kinetyczna byłaby wówczas mniejsza od zera.

Cząstkę taką można traktować jak piłkę toczącą się wewnątrz dołka. Piłka będzie wtaczać się na ściankę dołka tylko do momentu, w którym straci całą energię kinetyczną.

Cząstka kwantowa w dole potencjału

Cząstka α uwalniająca się z potencjału jądra (zielona linia) dzięki zjawisku tunelowemu

W zakresie odległości porównywalnych z rozmiarem atomu dominuje opis kwantowomechaniczny z zastosowaniem praw mechaniki kwantowej ^[1]. Za cząstkę kwantową można uważać elektron w stanie stacjonarnym w potencjale atomu lub nukleon w potencjale jądra . W mechanice kwantowej cząstka nie jest bryłą sztywną o określonej wielkości i sprecyzowanym położeniu, choć interpretacja funkcji falowej stanu stacjonarnego powinna skłaniać do przeciwnego wniosku (jeżeli funkcję falową interpretować jako falę mechaniczną, wówczas cząstka powinna się znajdować zawsze pośrodku jamy potencjału; stacjonarność rozwiązań w dowolnej chwili pozbawiłaby cząstkę jakiegokolwiek ruchu, jeżeli tej nie towarzyszyłaby zmiana poziomów energetycznych). Jest reprezentowana przez funkcję falową , która określa prawdopodobieństwo lokalizacji cząstki w określonym obszarze przestrzeni poprzez kwadrat funkcji falowej w tym obszarze.

Postać funkcji falowej w konkretnym obszarze przestrzeni zakłada się, a następnie rozwiązuje równanie Schrödingera dla tego obszaru. Jeżeli analizowany jest jednowymiarowy ruch cząstki, czyli tylko wzdłuż wyróżnionej osi, w polu zadanego potencjału, wówczas do opisu stosuje się równanie Schrödingera w postaci

Jest to tak zwane równanie Schrödingera bez czasu ze stacjonarnym, czyli niezależnym od czasu rozwiązaniem odpowiadającym fali stojącej i stałą energią stanu cząstki. Zakłada się, że wewnątrz dołu potencjału równanie to ma rozwiązanie w postaci superpozycji dwu^[2] funkcji falowych interpretowanych jako fale biegnące w przeciwnych kierunkach; dodatnim i ujemnym wzdłuż osi OX

Zakłada się istnienie rozwiązania równania w postaci funkcji falowej w obszarze jamy potencjału, wewnątrz bariery^[3] z zespoloną wartością współczynnika k, która opisuje tłumienie fali w obszarze dużych wartości potencjału, jak i założoną postać funkcji falowej poza barierą, czyli

Poza barierą potencjału nie istnieje rozwiązanie, które można by interpretować jako falę odbitą, jeżeli miałaby to być jedyna bariera potencjału, dlatego funkcja falowa w tym obszarze nie jest superpozycją. Funkcja falowa musi pozostawać ciągła na granicy obszarów z różną wartością potencjału.

Z tego, że amplituda B jest mniejsza od amplitudy A, zaś kwadrat amplitudy funkcji falowej określa prawdopodobieństwo znalezienia cząstki w danym miejscu, wynika istnienie niezerowego prawdopodobieństwa, że rozwiązanie istnieje poza jamą potencjału, czyli niezerowe prawdopodobieństwo znalezienia tam cząstki.

Współczynnik przenikania

Prawdopodobieństwo przeniknięcia cząstki przez barierę potencjału równe jest ilorazowi kwadratów amplitud B i A

i nazywany jest współczynnikiem przenikania lub współczynnikiem transmisji. Wartość tego współczynnika zależy od energii stanu stacjonarnego cząstki, wysokości i rozciągłości oraz kształtu bariery potencjału, w tym od względnej energii cząstki w obszarze jamy potencjału. Przybliżony wzór na współczynnik przenikania dla bariery o dowolnym kształcie ma postać

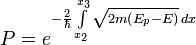
Ciągłe i skomplikowane zmiany potencjału przybliża się obszarami założonych stałych wartości potencjału - przybliżenie WKB.

Pojedyncza bariera

Jeżeli cząstka porusza się swobodnie napotykając po drodze barierę potencjału, wówczas może odbić się od bariery, lub ją pokonać. Jeżeli cząstka porusza się wzdłuż osi OX w prawo, wówczas po lewej stronie od bariery rozwiązanie będzie superpozycją funkcji falowych dla cząstki padającej i odbitej

Natomiast po prawej stronie bariery, podobnie jak dla cząstki uwalniającej się z dołu potencjału, funkcja falowa będzie miała postać

Współczynnik przenikania będzie teraz wyrażony wzorem

Natomiast wielkość

nazywamy współczynnikiem odbicia cząstki od bariery.

Współczynniki odbicia i transmisji cząstki przez barierę mogą być wyznaczane zarówno w przypadku, gdy bariera ma większą wysokość od energii cząstki jak i wówczas gdy bariera jest niższa od tej energii. W fizyce klasycznej brak odpowiednika przykładu z wydostawaniem się cząstki z obszaru, w którym energia stanu stacjonarnego jest mniejsza niż wysokość bariery energetycznej. Podobnie nie jest możliwe, aby klasyczna cząstka odbijała się od bariery potencjału, gdy ma energię wystarczającą do jej pokonania.

Gdy bariera potencjału jest większa od energii cząstki, wówczas prawdziwa jest relacja

w przeciwnym wypadku

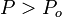
Interpretacja w oparciu o zasadę nieoznaczoności

Efekt tunelowy można wyjaśnić również bez odwoływania się do pojęcia funkcji falowej tylko na podstawie zasady nieoznaczoności . Zgodnie z tą zasadą iloczyn niepewności energii i czasu pomiaru energii musi spełniać warunek

Wynika stąd, że przez pewien krótki moment energia cząstki może wzrosnąć na tyle, że będzie większa od wysokości bariery potencjału i cząstka może znaleźć się po drugiej stronie bariery. W tej interpretacji zjawisko to nie będzie przenikaniem, a raczej wirtualnym (krótkoczasowym) przeskakiwaniem nad przeszkodą. O ile sam przeskok pozostaje wirtualny, o tyle zlokalizowanie cząstki poza przeszkodą jest już zupełnie realne. Rachunki na konkretnym przykładzie mogą jednak prowadzić do wniosku, że czas istnienia takiej fluktuacji jest krótszy niż czas propagacji na odległość równą rozległości bariery potencjału.

Efekt tunelowy w przyrodzie i w technice

Fuzja jądrowa będąca źródłem energii Słońca zachodzi w dużym stopniu dzięki zjawisku tunelowemu. Zjawisko to umożliwia pokonanie bariery odpychania kulombowskiego jąder atomów w temperaturze niższej, niż wynikałoby to z praw termodynamiki . Efekt tunelowy stwarza również nadzieje na obniżenie temperatury fuzji przeprowadzanej w sposób kontrolowany . Dzięki zjawisku tunelowemu następuje emisja cząstek α w procesie rozpadu promieniotwórczego masywnych jąder atomowych.

We współczesnej technice na zjawisku tunelowym oparte jest funkcjonowanie wielu półprzewodnikowych elementów elektronicznych (np. dioda tunelowa ) oraz urządzeń takich jak skaningowy mikroskop tunelowy .

Przypisy

Źródła

1. I.W. Sawieliew, Wykłady z fizyki t. 3, PWN, Warszawa 1994,
2. Jay Orear, Fizyka t.2, Wydawnictwo Naukowo-Techniczne, Warszawa 1998,