|
Indukcja pozaskończona
Indukcja pozaskończonaW
teorii mnogości
, indukcja pozaskończona to rozszerzenie
indukcji matematycznej
na zbiory
dobrze uporządkowane
, czy też nawet na klasę
liczb porządkowych
. WstępZarówno definicje indukcyjne jak i twierdzenie o indukcji matematycznej można porównać do rozumowań krok po kroku, gdzie kroki są ponumerowane
liczbami naturalnymi
. Np sedno dowodów indukcyjnych leży zawsze w podaniu uzasadnienia, że dla każdego  , , jeśli do kroku n (wyłącznie) wszystko było dobrze, to stąd można wywnioskować, że na kroku n też wszystko jest dobrze.Możemy jednak sobie wyobrazić, że wykonaliśmy wszystkie kroki ponumerowane liczbami naturalnymi i chcemy kontynuować nasz proces. Ponieważ jedyną własnością liczb naturalnych potrzebną do rozumowań indukcyjnych jest, że każdy niepusty podzbiór 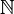 ma
element najmniejszy
, naturalnym sposobem na kontynuację naszego procesu, jest deklaracja, że nasze kroki są numerowane przez kolejne elementy pewnego zbioru dobrze uporządkowanego. Ale przecież każdy zbiór dobrze uporządkowany jest porządkowo izomorficzny z pewną liczbą porządkową (której elementy to liczby porządkowe od niej mniejsze). Zatem możemy myśleć, że nasze kroki w procesie indukcyjnym są ponumerowane liczbami porządkowymi. Wówczas sedno rozszerzonych dowodów indukcyjnych (czyli dowodów przez indukcję pozaskończoną) leży w podaniu uzasadnienia, że dla każdej liczby porządkowej α, ma
element najmniejszy
, naturalnym sposobem na kontynuację naszego procesu, jest deklaracja, że nasze kroki są numerowane przez kolejne elementy pewnego zbioru dobrze uporządkowanego. Ale przecież każdy zbiór dobrze uporządkowany jest porządkowo izomorficzny z pewną liczbą porządkową (której elementy to liczby porządkowe od niej mniejsze). Zatem możemy myśleć, że nasze kroki w procesie indukcyjnym są ponumerowane liczbami porządkowymi. Wówczas sedno rozszerzonych dowodów indukcyjnych (czyli dowodów przez indukcję pozaskończoną) leży w podaniu uzasadnienia, że dla każdej liczby porządkowej α, jeśli do kroku α (wyłącznie) wszystko było dobrze, to stąd można wywnioskować, że na kroku α też wszystko jest dobrze. TwierdzeniaNiech ON oznacza klasę liczb porządkowych. Poniższe twierdzenia można udowodnić w
ZF
(bez użycia
aksjomatu wyboru
). Twierdzenie o dowodzeniu przez indukcjęPrzypuśćmy, że  jest
formułą
języka teorii mnogości z jedną zmienną wolną x. Załóżmy również, że dla każdej liczby porządkowej α zachodzi implikacja jest
formułą
języka teorii mnogości z jedną zmienną wolną x. Załóżmy również, że dla każdej liczby porządkowej α zachodzi implikacja 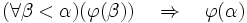 . .
Wówczas jest prawdziwe, że  . . Powyższe twierdzenie formułuje się też w następujący sposób: każda niepusta klasa liczb porządkowych ma element najmniejszy. Dowód: Przypuśćmy, że istnieje taka liczba porządkowa α0, że  . Wówczas zbiór . Wówczas zbiór  jest niepusty. Wiadomo, że każda niepusta podklasa klasy wszystkich liczb porządkowych ma element najmniejszy, więc niech β = minU. Jeśli γ < β, to również γ < α0, a więc na mocy założenia jest niepusty. Wiadomo, że każda niepusta podklasa klasy wszystkich liczb porządkowych ma element najmniejszy, więc niech β = minU. Jeśli γ < β, to również γ < α0, a więc na mocy założenia 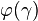 . Pokazuje to, że . Pokazuje to, że  . Na mocy założenia, zachodzi także . Na mocy założenia, zachodzi także  – sprzeczność. – sprzeczność. Twierdzenie o definicji indukcyjnejPrzypuśćmy, że 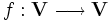 jest klasą, która jest też funkcją. Wówczas istnieje jedyna funkcja jest klasą, która jest też funkcją. Wówczas istnieje jedyna funkcja  (tak więc g jest też klasą) taka, że (tak więc g jest też klasą) taka, że  . .
Uwagi o stosowaniu- W twierdzeniu o definicji indukcyjnej, funkcja f reprezentuje przepis na konstrukcję obiektu związanego z liczbą α przy założeniu, że skonstruowaliśmy już ciąg
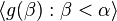 . . - W praktyce matematycznej, obydwa twierdzenia (zarówno o dowodzeniu jak i o definiowaniu indukcyjnym) są stosowane w odniesieniu do zbioru liczb porządkowych, często więc do liczb porządkowych mniejszych od pewnej ustalonej liczby
 . Wówczas w przypadku definicji indukcyjnej zarówno wyjściowa funkcja f jak i konstruowana funkcja g są zwykle zbiorami (a dziedziną tej ostatniej jest często właśnie liczba γ). . Wówczas w przypadku definicji indukcyjnej zarówno wyjściowa funkcja f jak i konstruowana funkcja g są zwykle zbiorami (a dziedziną tej ostatniej jest często właśnie liczba γ). - Istnieją jednak sytuacje gdy indukcja jest robiona po wszystkich liczbach porządkowych. Tak się dzieje przy definiowaniu
skali alefów
,
skali betów
czy też
uniwersum konstruowalnego
(i przy wykazywaniu pewnych ich własności).
- Czasami, ze względu na różny charakter argumentacji, dowody indukcyjne są podzielone na różne rodzaje kroków, typowo następujące trzy:
- Krok 0: pokazujemy, że
 jest prawdziwe, jest prawdziwe, - Krok następnikowy: pokazujemy, że jeśli
 jest prawdziwe, to również jest prawdziwe, to również 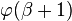 zachodzi, zachodzi, - Krok graniczny: pokazujemy, że jeśli α jest liczbą graniczną oraz
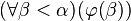 jest prawdziwe, to również jest prawdziwe, to również 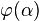 jest prawdziwe. jest prawdziwe.
- Wprawdzie same twierdzenia o indukcji nie wymagają AC, to często w ich zastosowaniach zakłada się ten aksjomat. Jest to zwykle spowodowane faktem, że musimy przetłumaczyć problem dotyczący jakiegoś zbioru A na problem o liczbach porządkowych, a to tłumaczenie osiągamy przez ponumerowanie elementów A przy użyciu liczb porządkowych. (Innymi słowy, zwykle najpierw musimy dobrze uporządkować rozważany obiekt, do czego jest potrzebny aksjomat wyboru.)
- W twierdzeniu o definicji indukcyjnej, właściwie nie można wyrażać jedyności funkcji w języku ZFC. Formalnie, można udowodnić następujące schematy twierdzeń:
- (istnienie) Dla każdej klasy f (danej przez formulę φf(x,y)) można znaleźć klasę g (danej przez formulę φg) taką, że
- Jeśli
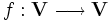 jest funkcją, to też g jest funkcją jest funkcją, to też g jest funkcją  i i  . .
- (jedyność) Dla każdej klasy f, g, g' :
- Jeśli
 i także i także  , , - to g(α) = g'(α) dla każdego α. (W tym drugim schemacie używamy twierdzenia o dowodzeniu przez indukcję.)
Przykłady zastosowania indukcji pozaskończonejDefinicje indukcyjne: - Konstrukcja
zbioru Bernsteina
,
- Konstrukcja przestrzeni Novaka,
- Definicja
hierarchii borelowskiej
,
- Definicja
termów booleowskich
,
- Definicja
skali alefów
,
- Definicja
skali betów
,
- Definicje
dodawania, mnożenia i potęgowania
liczb porządkowych,
- Definicja
klas Baire'a
(dla funkcji pomiędzy
przestrzeniami polskimi
),
- Definicja
uniwersum konstruowalnego
,
- Definicja
szerokości Cantora-Bendixsona przestrzeni rozproszonej
.
Zobacz też
Inne hasła zawierające informacje o "Indukcja pozaskończona":
Arystoteles
...
Rozumowanie
...
Indukcja pozaskończona
W
teorii mnogości
, Indukcja pozaskończona to rozszerzenie
indukcji matematycznej
na zbiory
dobrze uporządkowane
, czy też ...
Ludwik Gumplowicz
...
Liczba pierwsza
...
Metodologia historii
...
Indukcja
matematyczna
- pojęcie w matematyce określające metodę dowodzenia twierdzeń i konstrukcji pewnych obiektów.
Indukcja pozaskończona
- uogólnienie indukcji matematycznej używane głównie w teorii mnogości. ...
Spektroskopia EPR
...
Magnetyzacja
...
Efekt Zeemana
...
Inne lekcje zawierające informacje o "Indukcja pozaskończona":
135 Nauka, technika i kultura przełomu XIX i XX wieku (plansza 4)
...
023. F. Bacon i indukcja eliminacyjna (plansza 17)
...
203 Okres międzywojenny na świecie. Postęp techniczny i kryzys gospodarczy (plansza 2)
...
|