Równanie Bernoulliego - jedno z podstawowych równań hydrodynamiki płynów idealnych, sformułowane przez Daniela Bernoulliego w 1738 roku.

Równanie Bernoulliego opisuje zachowanie gęstości energii całkowitej na linii prądu . Obowiązuje w podstawowej wersji dla stacjonarnego przepływu nieściśliwego płynu idealnego , a w wersji rozszerzonej dla idealnego płynu barotropowego . Równanie Bernoulliego wynika z zasady zachowania energii i według intencji jego autora stanowić powinno jej zapis za pomocą parametrów hydrodynamicznych (p. zastrzeżenia podane poniżej w Uwagach dotyczących zastosowania równania Bernoulliego).

Równanie Bernoulliego stanowi całkę bardziej ogólnego hydrodynamicznego równania Eulera.

Szczególna postać równania

Założenia:

• ciecz jest nieściśliwa
• ciecz nie jest lepka
• przepływ jest stacjonarny i bezwirowy

Przy powyższych założeniach równanie przyjmuje postać:

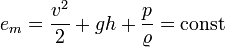
gdzie:

• - energia jednostki masy płynu,
• - gęstość płynu,
• - prędkość płynu w rozpatrywanym miejscu,
• - wysokość w układzie odniesienia, w którym liczona jest energia potencjalna ,
• - przyspieszenie grawitacyjne ,
• - ciśnienie płynu w rozpatrywanym miejscu.

Poszczególne człony równania to kolejno: energia kinetyczna , energia potencjalna grawitacji, energia ciśnienia.

Energia jest stała tylko wówczas, kiedy element porusza się wzdłuż linii prądu. W rozważanym przypadku zapewnia to stacjonarność przepływu. Istnienie lepkości lub przepływu wirowego rozprasza energię, ściśliwość zmienia zależność prędkości przepływu od ciśnienia. Niestacjonarność przepływu wiąże się z dodatkowym ciśnieniem rozpędzającym lub hamującym ciecz.

Ogólna postać równania

Równanie Bernoulliego może być z pewną dokładnością stosowane także dla idealnych płynów ściśliwych ale tylko typu barotropowego . Opracowano również wersję równania dla płynów uwzględniającą zmianę energii wewnętrznej płynu w wyniku różnych czynników. Równanie to w ogólności ma postać:

Gdzie:

• - energia potencjalna jednostki masy, której w warunkach ziemskich odpowiada
• - entalpia przypadająca na jednostkę masy (entalpia właściwa)

przy czym - energia wewnętrzna płynu.

Uwzględniając właściwości gazów można przekształcić to równanie tak, by było spełnione także dla gazów. Choć pierwotne równanie Bernoulliego nie jest spełnione dla gazów, to ogólne wnioski płynące z niego mogą być stosowane również dla nich.

Praktyczne wykorzystanie równania Bernoulliego

Z równania Bernoulliego dla sytuacji przedstawionej na rysunku zachodzi prawidłowość:

Jeżeli zaniedbać zmianę wysokości odcinków rury, to wzór upraszcza się do:

W rurze o mniejszym przekroju ciecz płynie szybciej (), w związku z tym panuje w niej mniejsze ciśnienie niż w rurze o większym przekroju.

Ciecz płynąc w rurze o zmieniającym się przekroju ma mniejsze ciśnienie na odcinku, gdzie przekrój jest mniejszy.

Podana wyżej własność cieczy była znana przed sformułowaniem równania przez Bernoulliego i nie potrafiono jej wytłumaczyć, stwierdzenie to i obecnie kłóci się ze "zdrowym rozsądkiem" wielu ludzi i dlatego znane jest pod nazwą paradoks hydrodynamiczny .

A także: Ciecz opływając ciało zanurzone w cieczy wywołuje mniejsze ciśnienie od strony gdzie droga przepływu jest dłuższa.

Zastosowanie równania Bernoulliego

Równaniem Bernoulliego opisuje wiele na co dzień obserwowanych zjawisk, zależności, a także zasad działania licznych urządzeń technicznych:

• paradoks hydrodynamiczny
• zjawisko zrywania dachów, gdy wieje silny wiatr
• zasada działania rurki Pitota
• zasada działania rurki Prandtla
• zasada działania zwężki Venturiego
• zasada działania palnika Bunsena
• pośrednio zasady powstawania siły nośnej w skrzydle samolotu
• pośrednio w powstawaniu efektu Magnusa
• przyczyna osiadania statków w ruchu na płytkim akwenie.

Uwagi dotyczące stosowania równania Bernoulliego

Równanie Bernoulliego nie uwzględnia tarcia wewnętrznego w płynie przejawiającego się w postaci lepkości , a tym samym nie odzwierciedla poprawnie zasady zachowania energii, którą miało reprezentować w intencji jego autora. Dlatego też równanie Bernoulliego stosować można jedynie w sytuacjach, w których efekty związane z lepkością płynu nie odgrywają istotnej roli. W przeciwnym przypadku bezpośrednie stosowanie równania Bernoulliego prowadzi do paradoksów lub wyników w drastyczny sposób sprzecznych z doświadczeniem. Przykładem jest paradoks przepływu w rurze o stałym przekroju, zgodnie z którym, w przepływającym w rurze płynie, nie następuje spadek ciśnienia, czemu przeczą wszelkie obserwacje doświadczalne.

Bibliografia