Trójwymiarowa ilustracja wzoru Eulera
Wzór Eulera – wzór
analizy zespolonej
wiążący
funkcje trygonometryczne
z
zespoloną
funkcją wykładniczą
określany nazwiskiem
Leonharda Eulera
.
Wzór
Niech 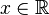 , zaś
, zaś 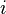 jest
jednostką urojoną
, wtedy wzór Eulera ma postać
jest
jednostką urojoną
, wtedy wzór Eulera ma postać
 .
.
Historia
Wzór Eulera został
dowiedziony
po raz pierwszy przez
Rogera Cotesa
w
1714
w postaci

Euler był pierwszym, który opublikował go w obecnie stosowanej formie w
1748
, opierając swój dowód na równości
szeregów
po obu stronach tożsamości. Żaden z nich nie widział interpretacji geometrycznej tego wzoru: utożsamienie
liczb zespolonych
z
płaszczyzną zespoloną
powstało około 50 lat później (wynik
Caspara Wessela
).
Dowód
Wzór można otrzymać określając potęgi zespolone liczby
e
. Rozwinięte w
szereg potęgowy
funkcje  przyjmują wtedy postać:
przyjmują wtedy postać:
 ,
, ,
, .
.
Powyższe definicje są poprawne również dla liczb zespolonych, gdyż
promień zbieżności
każdego szeregów jest nieskończony. Aby odróżnić przypadek rzeczywisty od zespolonego za 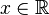 podstawione zostanie
podstawione zostanie  .
.
Potęgę eiz definiuje następujący wzór:
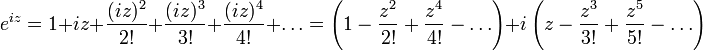 ,
,
czyli eiz = cosz + isinz.
Ponieważ każdy z szeregów jest
zbieżny bezwzględnie
, to można zmieniać kolejność wyrazów bez zmiany sumy szeregu. Powrót do liczb rzeczywistych za pomocą podstawienia 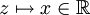 daje oryginalną tożsamość odkrytą przez Eulera.
daje oryginalną tożsamość odkrytą przez Eulera.
- Inne uzasadnienie formuły
Niech  będzie dana przez
będzie dana przez  . Wówczas
. Wówczas
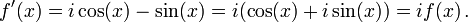
Następnie niech g(x) = e − ixf(x). Wtedy

dla każdego x, a stąd g jest funkcją stałą. Ponieważ
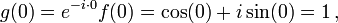
mamy g(x) = 1 dla wszystkich x. Stąd też f(x) = g(x)eix = eix, czyli
 .
.
Przy okazji warto zauważyć, że jest to
postać trygonometryczna
liczby zespolonej
o
module
jednostkowym.
Trygonometria
Wzór Eulera stanowi powiązanie analizy i trygonometrii dostarczając interpretację funkcji
sinus i cosinus
jako sum ważonych
funkcji wykładniczej
. Odpowiednie wzory można wyprowadzić budując odpowiedni układ równań:
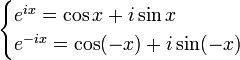 .
.
Korzystając z własności
parzystości i nieparzystości
funkcji trygonometrycznych:
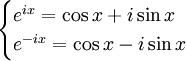 .
.
Po dodaniu stronami:
- eix + e − ix = 2cosx
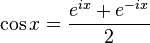
Analogicznie otrzymuje się wzór:
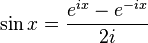 .
.
Wzory te mogą służyć jako definicje funkcji trygonometrycznych dla argumentów zespolonych. Przykładowo podstawienie x = iy daje:
 ,
,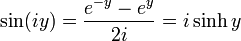 .
.
Zastosowanie
Tożsamość może zostać wykorzystana jako metoda do upraszczania wyrażeń trygonometrycznych. Wymaga ona co prawda przejścia w rachunkach przez
liczby zespolone
, ale nie wymaga żadnej wiedzy na ich temat oprócz pamiętania, że i2 = − 1 i znajomości poniższych trzech wzorów (funkcje tangens i cotangens określa się tak samo jak w przypadku rzeczywistym):
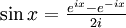


Najpierw należy przekształcić upraszczany wzór za pomocą dwóch pierwszych wzorów na postać wykładniczą (w przypadku tangensa i cotangensa rozbijając go na iloraz funkcji sinus i cosinus), następnie wykonać odpowiednie działania tak, jak na zwykłych potęgach liczb rzeczywistych, a na koniec stosując jeden z wzorów Eulera wrócić do postaci trygonometrycznej wyrażenia.
Przykłady
- Sinus kąta zwielokrotnionego
Dla całkowitych dodatnich n wyrażenia postaci sinnx dają się wyrazić za pomocą samych wartości sinx i cosx oraz elementarnych działań.
Korzystając z powyższych wzorów:
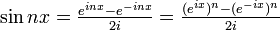
Ze wzoru Eulera:

Z
dwumianu Newtona
:

Wyłączając wspólny czynnik:
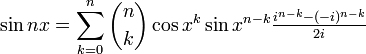
I stosując wzór Eulera dostajemy ostatecznie

Kilka pierwszych wielokrotności:
- sin2x = 2cosxsinx
- sin3x = 3cos2xsinx − sin3x
- sin4x = 4cos3xsinx − 4cosxsin3x
- sin5x = 5cos4xsinx − 10cos2xsin3x + sin5x
- Upraszczanie wyrażeń trygonometrycznych
Sprowadzić do prostszej postaci wyrażenie:
- f(x) = 8cos3xsinx − 4cosxsinx
Korzystając ze wzorów Eulera na sinus i cosinus:

Po wymnożeniu jest:

i dalej:
 ,
,
po skróceniu:
 ,
,
dlatego po zastosowaniu pierwszego z podanych wzorów Eulera wyrażenie ma postać:
- f(x) = sin4x
Tożsamość Eulera
Funkcja
wykładnicza
ez może być zdefiniowana jako
granica ciągu
(1+
z/N)
N, przy N dążącym do nieskończoności. Powyżej, kładziemy
z=iπ i rozważamy wartości N od 1 do 100. Obliczanie wartości (1+
iπ / N)
N jest przedstawione jako N-krotne powtórzenie możenia na
płaszczyźnie zespolonej
(gdzie ostatni punkt to wartość (1+
iπ / N)
N). Zauważmy, że ze zwiększaniem liczby N, liczba zespolona (1+
iπ / N)
N zbliża się do -1. Zatem
eiπ=-1.
W szczególności, podstawiając x = π otrzymuje się równość:
- eπi + 1 = 0,
nazywaną też tożsamością Eulera (czasami wzorem Eulera).
Nie istnieją żadne znane dokumenty potwierdzające autorstwo Eulera; co więcej, była ona zapewne znana matematykom żyjącym przed nim.
„Najpiękniejszy wzór”
Tożsamość Eulera nazywana jest często
najpiękniejszym
wzorem matematycznym. Wykorzystane są w niej trzy
działania
arytmetyczne
:
dodawanie
,
mnożenie
i
potęgowanie
. Tożsamość łączy pięć fundamentalnych
stałych matematycznych
:
Dodatkowo każde z powyższych działań oraz każda ze stałych użyte są dokładnie raz, co więcej: wzór ten jest przedstawiony w zwyczajowej formie
równania
, którego prawa strona jest równa zeru.
Uogólnienie
Tożsamość Eulera jest przypadkiem szczególnym ogólniejszej tożsamości, w której
pierwiastki z jedynki
n-tego stopnia sumują się do 0 dla n > 1:
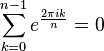 .
.
Tożsamość Eulera otrzymuje się przez podstawienie n = 2. Powyższą równość można zapisać i w postaci:
 .
.
ponieważ: exp(2πi) = 1.
Zobacz też