Zawieranie się zbiorów i ogólniej – klas liczbowych w sobie. Symbol

oznacza tu, że można skonstruować
klasę
liczb

tak, aby była podklasą klasy
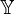
. Zbiory umieszczone na rysunku powyżej liczb zespolonych noszą wspólną nazwę
liczb hiperzespolonych
. Na niebiesko oznaczone są rodzaje liczb które nie tworzą zbiorów, lecz klasy właściwe. Liczby algebraiczne całkowite nie są szczególnym przypadkiem liczb algebraicznych rzeczywistych – to nie jest pomyłka. Zobacz sekcję
Liczby algebraiczne
.
Liczba – pojęcie abstrakcyjne, jedno z najczęściej używanych w
matematyce
. Pierwotnie liczby służyły do porównywania wielkości zbiorów przedmiotów (
liczby naturalne
), później także wielkości ciągłych (miary i wagi), obecnie w matematyce są rozważane jako twory abstrakcyjne, w oderwaniu od ewentualnych fizycznych zastosowań.
Określenie „liczba” bez żadnego przymiotnika jest nieścisłe, gdyż matematycy nie definiują „liczb”, lecz „liczby naturalne”, „liczby całkowite”, itp. Poszczególne rodzaje liczb są definiowane za pomocą
aksjomatów
lub konstruowane z bardziej podstawowych pojęć, takich jak
zbiór
, czy typy liczb prostsze od konstruowanego.
Zastosowania
Najprostsze rodzaje liczb, jak
liczby naturalne
czy
rzeczywiste
, są w powszechnym użyciu jako oznaczenia ilości przedmiotów (np. pięć jabłek) lub mnożnika pewnej
jednostki miary
(np. dwa i pół metra). Zapisy liczb naturalnych są używane także jako
identyfikatory
, np.
numery telefonów
, dróg,
PESEL
,
ISBN
.
W matematyce nauczane w szkołach podstawowych liczby naturalne, wymierne i rzeczywiste zostały rozszerzone na takie abstrakcje, jak
liczby zespolone
,
p-adyczne
,
kwaterniony
, czy
sedeniony
. Liczby zespolone okazały się przydatne w wielu dziedzinach od
grafiki komputerowej
[1], przez
elektronikę
[2],
teorię płynów
, aż do
fizyki kwantowej
[3] i
teorii względności
. Kwaterniony znalazły zastosowanie w
grafice trójwymiarowej
do prostego obliczania obrotów w przestrzeni (zob.
współrzędne jednorodne
).
Liczby p-adyczne
znalazły zastosowanie w
kryptografii
.
Opis intuicyjny
Poniższe opisy w żadnym wypadku nie są ścisłymi definicjami. Liczby są jednak w matematyce definiowane ściśle, i definicje te są przedstawione w
wydzielonym artykule
. Poniżej podane są opisy tylko kilku najprostszych zbiorów liczbowych.
Liczby naturalne
Najczęściej używanymi liczbami są liczby naturalne. Wśród matematyków istnieją dwie szkoły:
- Jedni uważają, że zero powinno zaliczać się do liczb naturalnych (a więc liczby naturalne to
 ). Takie podejście jest związane z najbardziej „naturalnym” zastosowaniem liczb naturalnych – zliczaniem elementów skończonych zbiorów. W życiu codziennym używa się liczb naturalnych głównie w tym właśnie celu, aby określić liczbę przedmiotów w jakiejś grupie. Zero odpowiada wtedy liczności
zbioru pustego
.
). Takie podejście jest związane z najbardziej „naturalnym” zastosowaniem liczb naturalnych – zliczaniem elementów skończonych zbiorów. W życiu codziennym używa się liczb naturalnych głównie w tym właśnie celu, aby określić liczbę przedmiotów w jakiejś grupie. Zero odpowiada wtedy liczności
zbioru pustego
. - Inni uznają, że liczby naturalne zaczynają się od jedynki. Liczba zero weszła do matematyki stosunkowo późno[4], być może więc wydaje się „mniej naturalna” od pozostałych liczb naturalnych.
Z punktu widzenia aksjomatyki kwestia zaliczenia zera do liczb naturalnych jest czysto umowna i nie sprawia żadnych problemów pod warunkiem konsekwentnego trzymania się tej umowy podczas rozumowania.
Liczby całkowite
Liczby ujemne
to liczby mniejsze od zera. Dla każdej dodatniej liczby (czyli większej od zera) można wskazać liczbę do niej przeciwną, czyli liczbę ujemną leżącą na osi liczbowej w tej samej odległości od zera. Ich suma zawsze daje zero: jeśli na konto wpłynie 100 zł, to w rachunkach można ten fakt zaznaczyć jako 100, wypłatę 100 zł można wtedy oznaczać liczbą ujemną -100. Liczby naturalne  , zero oraz liczby przeciwne do naturalnych
, zero oraz liczby przeciwne do naturalnych  znane są właśnie jako liczby całkowite.
znane są właśnie jako liczby całkowite.
Liczby wymierne
Liczby wymierne to intuicyjnie
ułamki
powstające przez podzielenie liczby całkowitej (zwanej licznikiem) przez liczbę całkowitą różną od zera (zwaną mianownikiem), np.  .
Dzielenie przez zero
jest operacją niewykonalną.
.
Dzielenie przez zero
jest operacją niewykonalną.
Ułamek  dla
dla 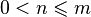 reprezentuje wielkość otrzymaną po podzieleniu całości na m równych części, a następnie wybraniu n spośród nich. Dwa różne ułamki mogą reprezentować tę samą liczbę wymierną, np.
reprezentuje wielkość otrzymaną po podzieleniu całości na m równych części, a następnie wybraniu n spośród nich. Dwa różne ułamki mogą reprezentować tę samą liczbę wymierną, np. 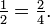 Każdy ułamek można jednak skrócić, tzn. podzielić licznik i mianownik przez tę samą liczbę całkowitą (ich
największy wspólny dzielnik
), tak aby dalsze dzielenie tych wielkości w zbiorze liczb całkowitych było już niemożliwe.
Każdy ułamek można jednak skrócić, tzn. podzielić licznik i mianownik przez tę samą liczbę całkowitą (ich
największy wspólny dzielnik
), tak aby dalsze dzielenie tych wielkości w zbiorze liczb całkowitych było już niemożliwe.
Jeśli licznik i mianownik są jednocześnie dodatnie lub jednocześnie ujemne, to reprezentowana przez ułamek liczba wymierna również jest dodatnia. Jeśli licznik jest zerem, to liczba wymierna jest zerem. Jeśli licznik ma znak przeciwny do znaku mianownika, to liczba wymierna nim wyrażona jest ujemna.
Jeśli n,m > 0 oraz n > m, to ułamek reprezentuje liczbę większą od 1. Jeśli n = km (gdzie k jest liczbą całkowitą), to ułamek reprezentuje liczbę całkowitą k.
Liczby wymierne są
uporządkowane liniowo
(każde dwie liczby wymierne są porównywalne). Jest to porządek gęsty: pomiędzy dwiema różnymi liczbami można zawsze znaleźć trzecią (a nawet nieskończoną ich liczbę).
Liczby rzeczywiste
Już starożytni
pitagorejczycy
odkryli, że istnieją liczby, których nie da się przedstawić w postaci ułamka  (takie jak np.
(takie jak np.  , czyli długość przekątnej kwadratu o boku jednostkowym), a więc nie są liczbami wymiernymi. Pitagorejczycy czcili liczby jako doskonałość i to odkrycie było dla nich szokiem. Fakt istnienia liczb niewymiernych był ich najgłębiej skrywaną tajemnicą[5][6].
, czyli długość przekątnej kwadratu o boku jednostkowym), a więc nie są liczbami wymiernymi. Pitagorejczycy czcili liczby jako doskonałość i to odkrycie było dla nich szokiem. Fakt istnienia liczb niewymiernych był ich najgłębiej skrywaną tajemnicą[5][6].
Liczby rzeczywiste to liczby wymierne oraz
liczby niewymierne
znajdujące się pomiędzy liczbami wymiernymi, lecz nie dające wyrazić się w postaci ułamka, takie jak  czy
π
. Każdej liczbie rzeczywistej odpowiada
punkt
na
prostej
(tzw.
oś liczbowa
).
czy
π
. Każdej liczbie rzeczywistej odpowiada
punkt
na
prostej
(tzw.
oś liczbowa
).
Każda liczba rzeczywista jest
punktem skupienia
zbioru liczb wymiernych i liczby wymierne są
gęstym
podzbiorem zbioru liczb rzeczywistych.
Liczby zespolone
Liczby urojone
to liczby, których
kwadraty
są niedodatnimi liczbami rzeczywistymi. W szczególności jedną z nich jest tzw.
jednostka urojona
i, dla której i2 = − 1. Żadna liczba urojona oprócz zera nie jest równocześnie liczbą rzeczywistą.
Liczby zespolone to liczby powstające przez zsumowanie liczby rzeczywistej i liczby urojonej, np. 2 + 3i. W szczególności liczby rzeczywiste oraz liczby urojone także są liczbami zespolonymi (np. 5 = 5 + 0i). Każdej liczbie zespolonej odpowiada punkt na
płaszczyźnie
(tzw.
płaszczyzna zespolona
), a dodawanie i mnożenie są interpretowane geometrycznie.
Liczby algebraiczne
Liczba algebraiczna to taka liczba zespolona, która podstawiona do jakiegoś
wielomianu
o wymiernych współczynnikach (np. 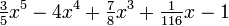 ) da w wyniku zero. W szczególności każda liczba wymierna
) da w wyniku zero. W szczególności każda liczba wymierna 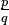 jest algebraiczna, bo jest pierwiastkiem wielomianu qx − p.
jest algebraiczna, bo jest pierwiastkiem wielomianu qx − p.
Liczby przestępne
Liczby przestępne to liczby zespolone nie będące algebraicznymi. Słynnymi przykładami liczb przestępnych są
π
oraz
e
.
Oznaczenia zbiorów liczbowych
W matematyce powszechnie przyjęte są pewne oznaczenia zbiorów liczbowych. W polskich gimnazjach i szkołach średnich korzysta się z symboli nawiązujących do polskich nazw zbiorów, jednak w szkołach wyższych i środowisku naukowym (a także tym i pozostałych artykułach Wikipedii) korzysta się z oznaczeń międzynarodowych.
| Zbiór | Oznaczenie „szkolne” | Oznaczenie standardowe | Uwagi |
|---|
| Liczby naturalne bez zera |  |  , czasem , czasem  | rzadziej używane oznaczenia:  |
| Liczby naturalne z zerem | 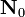 , czasem , czasem  |  , czasem , czasem  | w
teorii mnogości
ω |
| Liczby całkowite |  |  | od
niem.
Zahlen – liczby |
| Liczby wymierne |  |  | od
niem.
Quotient – iloraz[7] |
| Liczby niewymierne | czasem 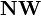 | 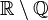 | |
| Liczby rzeczywiste |  |  | od ang. real numbers |
| Liczby algebraiczne | | czasem 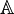 | |
| Liczby zespolone | 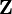 |  | od ang. complex numbers |
| Kwaterniony | | 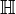 | od ang. Hamilton numbers – liczby Hamiltona |
| Oktoniony | |  | znane również jako oktawy Cayleya |
| Sedeniony | |  | |
| Liczby p-adyczne | |  | |
Własności algebraiczne
Działania
na liczbach, takie jak
dodawanie
,
odejmowanie
,
mnożenie
czy
dzielenie
można zdefiniować także w zbiorach, które nie mają z liczbami wiele wspólnego, jak
symetrie
wielościanów
w przestrzeni, o ile tylko działania te będą tam miały podobne właściwości, np. będą
przemienne
, czy
łączne
.
Struktury algebraiczne
, w których działania mają pewne określone właściwości, posiadają w
algebrze
własne nazwy, takie jak
grupa
,
pierścień
czy
ciało
.
Liczby na ogół definiowane są krok po kroku. Rozpoczyna się od liczb naturalnych, następnie rozszerza ich algebrę na liczby całkowite, wymierne, rzeczywiste, zespolone…
Struktury algebraiczne
liczb całkowitych i wymiernych rozszerzają kolejno strukturę liczb naturalnych tak, aby najprostsze działania arytmetyczne dawały się w nich wykonać dla dowolnych dwóch liczb (z wyjątkiem
dzielenia przez zero
). Działania takie nazywa się
działaniami wewnętrznymi
danego zbioru liczbowego, gdyż ich wynik zawsze będzie zawarty w tym zbiorze, dlatego mówi się też, że zbiór jest zamknięty ze względu na dane działanie. Kolejne rozszerzenia – na liczby rzeczywiste i zespolone – wzbogacają strukturę algebraiczną o dalsze interesujące właściwości.
- Dla liczb naturalnych (z zerem lub bez niego) działaniami wewnętrznymi są np. dodawanie i mnożenie. Dodanie lub pomnożenie przez siebie dwóch liczb naturalnych daje zawsze liczbę naturalną. Dla dodawania i mnożenia można skonstruować działania odwrotne – odejmowanie i dzielenie. Jednak odejmowanie większej liczby od mniejszej nie daje się wykonać w zbiorze liczb naturalnych, odejmowanie nie jest zatem działaniem wewnętrznym tego zbioru. Podobnie jest z dzieleniem.
- Rozszerzenie liczb naturalnych tak, aby odejmowanie było zawsze wykonalne, daje w rezultacie
pierścień
liczb całkowitych. Odejmowanie jest już dla nich działaniem wewnętrznym.
- Powiększenie pierścienia liczb całkowitych tak, aby wykonalne było dzielenie dowolnej liczby całkowitej przez dowolną niezerową liczbę całkowitą, prowadzi do tzw.
ciała
liczb wymiernych. Jego działaniami wewnętrznymi są dodawanie, odejmowanie, mnożenie oraz dzielenie przez liczbę niezerową.
- Liczby wymierne nie wyczerpują wszystkich możliwości. Jak już wspomniano wcześniej,
przekątna
kwadratu
o boku jednostkowym ma długość nie dającą się wyrazić liczbą wymierną. Również
pole powierzchni
koła
o
promieniu
jednostkowym nie daje się wyrazić taką liczbą. Pole to można jednak z dowolną dokładnością przybliżyć, pokrywając koło siatką przystających kwadratów o bokach będących liczbami wymiernymi i zliczając pola kwadratów mieszczących się w całości w tym kole. Następnie powtarzając tę operację dla coraz mniejszych kwadratów można utworzyć
ciąg
liczb wymiernych coraz lepiej przybliżających pole danego koła. Żądanie, aby dowolna skończona
granica ciągu
liczb wymiernych dawała się wyrazić liczbowo, prowadzi do rozszerzenia ciała liczb wymiernych do ciała liczb rzeczywistych.
-
Wielomiany
w zbiorze liczb rzeczywistych nie zawsze mają
pierwiastki
rzeczywiste – matematycy mówią, że ciało liczb rzeczywistych nie jest
algebraicznie domknięte
. Na przykład równanie x2 + 1 = 0 nie ma w tym zbiorze rozwiązań. Na mocy twierdzenia, iż każde ciało jest podciałem pewnego ciała algebraicznie domkniętego, zbiór liczb rzeczywistych można rozszerzyć tak, aby każdy wielomian stopnia co najmniej pierwszego jednej zmiennej miał pierwiastek w nowym ciele. Powyższa propozycja usprawiedliwia użycie tzw. liczb zespolonych.
- Zbiory liczbowe można rozszerzać w dalszym stopniu otrzymując tzw.
liczby hiperzespolone
, w tym:
kwaterniony
,
oktawy Cayleya
i
sedeniony
. Zbiory te mają jednak coraz gorsze właściwości algebraiczne: kwaterniony nie tworzą już ciała, ponieważ mnożenie przestaje być przemienne, a w oktawach mnożenie przestaje być nawet łączne. Mimo wszystko liczby te znajdują swoje zastosowania. Więcej na ten temat znajduje się w artykule
aksjomaty i konstrukcje liczb
.
Odpowiednie własności działań w podstawowych zbiorach liczbowych zostały ujęte w tabeli (niżej legenda, oznaczenia wprowadzono wyłącznie na potrzeby artykułu):
| Zbiór liczbowy | Dodawanie | Odejmowanie | Mnożenie | Dzielenie |
|---|
| Liczby naturalne bez zera |  |  | 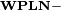 | 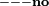 |
| Liczby naturalne z zerem | 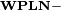 | 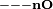 | 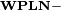 | 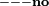 |
| Liczby całkowite |  |  | 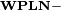 | 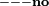 |
| Liczby wymierne |  |  |  |  |
| Liczby rzeczywiste |  |  |  |  |
| Liczby zespolone |  |  |  |  |
| Symbol | Własność | Definicja |
|---|
Legenda: 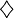 oznacza opisywane działanie, X to dany zbiór liczbowy oznacza opisywane działanie, X to dany zbiór liczbowy |
 |
Zamkniętość
zbioru na działanie. | 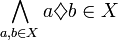 |
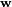 |
Zamkniętość
zbioru na dzielenie z wyłączeniem dzielenia przez zero. |  |
 |
Przemienność
działania | 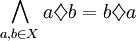 |
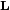 |
Łączność
działania | 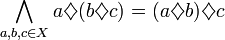 |
 | Obustronny
element neutralny
e działania w tym zbiorze. |  |
 | Wyłącznie prawostronny
element neutralny
dla wszystkich elementów zbioru. | 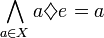 |
 | Obustronny
element odwrotny
dla wszystkich elementów zbioru. |  , gdzie e jest elementem neutralnym , gdzie e jest elementem neutralnym |
 | Obustronny
element odwrotny
dla wszystkich niezerowych elementów zbioru. |  , gdzie e jest elementem neutralnym , gdzie e jest elementem neutralnym |
Rodzaje struktur algebraicznych tworzonych przez poszczególne zbiory liczbowe z odpowiednimi działaniami:
- Dodawanie w zbiorze liczb naturalnych bez zera (jako działaniem łącznym i wewnętrznym) jest przykładem tzw.
półgrupy
.
- W zbiorze liczb naturalnych z zerem istnieje dodatkowo element neutralny dodawania (zero), w związku z czym ten zbiór z dodawaniem stanowi tzw.
monoid
.
- W zbiorze liczb całkowitych i szerszych, dodawanie jest odwracalne (dla każdego elementu x istnieje element y taki, że x + y = 0; element ten nazywa się elementem przeciwnym do x i oznacza przez − x). Zatem zbiór liczb całkowitych z dodawaniem tworzy
grupę przemienną
.
- Mnożenie we wszystkich tych zbiorach jest łączne, wewnętrzne i ma dokładnie jeden element neutralny, działanie to jednak nie jest odwracalne (zero nie ma elementu odwrotnego). Tworzy więc
monoid
.
- Dodawanie i mnożenie razem tworzą w zbiorze liczb naturalnych tzw. półpierścień
- Zbiór liczb całkowitych z dodawaniem i mnożeniem tworzy
dziedzinę całkowitości
.
- Począwszy od liczb wymiernych, zbiory z dodawaniem i mnożeniem razem tworzą już ciało – mnożenie z wyłączeniem zera jest odwracalne.
- Zbiory liczb wymiernych, rzeczywistych i zespolonych bez zera z mnożeniem tworzą grupę przemienną.
- Zbiór liczb rzeczywistych tworzy
przestrzeń liniową
nad ciałem liczb wymiernych.
- Ciało liczb rzeczywistych (i każde jego podciało) jest
ciałem formalnie rzeczywistym
, tj. element przeciwny jedynki nie jest sumą kwadratów niezerowych elementów ciała:
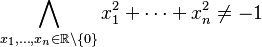 .
. - Ciało
 liczb rzeczywistych i ciało
liczb rzeczywistych i ciało 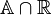 liczb rzeczywistych algebraicznych są ciałami
rzeczywiście domkniętymi
: tj. są ciałami formalnie rzeczywistymi, które nie posiadają rozszerzenia algebraicznego będącego ciałem formalnie rzeczywistym.
liczb rzeczywistych algebraicznych są ciałami
rzeczywiście domkniętymi
: tj. są ciałami formalnie rzeczywistymi, które nie posiadają rozszerzenia algebraicznego będącego ciałem formalnie rzeczywistym. - Zbiór liczb zespolonych tworzy przestrzeń liniową nad ciałem liczb rzeczywistych.
- Ciało
 liczb zespolonych i ciało
liczb zespolonych i ciało 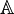 liczb algebraicznych są ciałami
algebraicznie domkniętymi
, tzn. każdy
wielomian
stopnia
co najmniej pierwszego jednej zmiennej z współczynnikami w
liczb algebraicznych są ciałami
algebraicznie domkniętymi
, tzn. każdy
wielomian
stopnia
co najmniej pierwszego jednej zmiennej z współczynnikami w  albo
albo 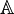 ma pierwiastek w odpowiednym ciele. W szczególności istnieje
ma pierwiastek w odpowiednym ciele. W szczególności istnieje  takie, że z2 = − 1. W ciele liczb zespolonych istnieją dokładnie dwie liczby o tej własności oznaczane i oraz − i.
takie, że z2 = − 1. W ciele liczb zespolonych istnieją dokładnie dwie liczby o tej własności oznaczane i oraz − i.
Ścisłe definicje liczb
Moce zbiorów liczbowych
Zbiory liczb naturalnych, całkowitych, wymiernych oraz algebraicznych są równoliczne, czyli mają tę samą
moc
; oznacza się ją za pomocą
hebrajskiej litery
alef
z zerem w indeksie (czyt. alef-zero), czyli  .
.
Zbiory o mocy nie większej niż  (w szczególności
zbiory skończone
) nazywane są
zbiorami przeliczalnymi
.
(w szczególności
zbiory skończone
) nazywane są
zbiorami przeliczalnymi
.
Zbiory liczb rzeczywistych, zespolonych, kwaternionów, oktonionów, sedenionów oraz liczb p-adycznych mają większą moc[8] –
continuum
– oznaczaną symbolem  . Kwestia, czy pomiędzy liczbą kardynalną
. Kwestia, czy pomiędzy liczbą kardynalną  a
a  jest jakakolwiek inna liczba kardynalna (tzw.
hipoteza continuum
) okazała się niemożliwa do wyprowadzenia z pozostałych
aksjomatów teorii mnogości
.
jest jakakolwiek inna liczba kardynalna (tzw.
hipoteza continuum
) okazała się niemożliwa do wyprowadzenia z pozostałych
aksjomatów teorii mnogości
.
Liczby kardynalne i opisane dalej liczby porządkowe nie tworzą w ogóle zbiorów. Założenie, że można utworzyć zbiór wszystkich liczb kardynalnych lub porządkowych prowadzi do sprzeczności (tzw.
paradoks Burali-Forti
).
Systemy liczbowe
System liczbowy to zbiór reguł do jednolitego zapisywania liczb. Generalnie systemy liczbowe można podzielić na pozycyjne i addytywne.
System zapisu liczb prekolumbijskich
Majów
opierał się na systemie piątkowym dla liczb 0-19. Większe liczby zapisywano używając potęg dwudziestki i powyższych symboli jako cyfr systemu dwudziestkowego
Pozycyjne systemy liczbowe
W
pozycyjnych systemach liczbowych
ten sam symbol (
cyfra
) ma różną wartość w zależności od pozycji, jaką zawiera w danej liczbie. Na przykład, w dziesiętnym zapisie liczby 11, pierwsza jedynka ma wartość 10, a druga 1, ze względu na inną ich pozycję w zapisie liczby.
Przykłady:
-
dziesiętny system liczbowy
, który jest współcześnie w powszechnym użyciu

-
dwójkowy system liczbowy
, czyli o podstawie 2, stosowany w
elektronice cyfrowej
, np. w
komputerach
. Przyczyną jest prostsza budowa i większa odporność na błędy
bramek logicznych
(elementów z których budowany jest
układ cyfrowy
) przy mniejszej liczbie możliwych stanów. Ponieważ najmniejsza użyteczna liczba stanów to dwa, więc najtaniej i najprościej zbudować układy cyfrowe oparte na systemie dwójkowym.


-
szesnastkowy system liczbowy
, w którym liczbom 10 do 15 odpowiadają cyfry oznaczane pierwszymi (małymi lub dużymi) literami alfabetu. Najczęściej używany w informatyce ze względu na oszczędność miejsca przy notowaniu, ponieważ każdy
bajt
może być zakodowany dwiema cyframi szesnastkowymi oraz łatwe konwersje do/z systemu dwójkowego – cyfrze szesnastkowej odpowiadają cztery cyfry dwójkowe (z podobnych względów używa się czasem
ósemkowego systemu liczbowego
).

W pozycyjnych systemach liczbowych o podstawie k każda nieujemna liczba rzeczywista x może być rozwinięta przy pomocy szeregu:

gdzie ci to cyfry będące liczbami naturalnymi z przedziału od 0 do k − 1.
Skrótowo liczbę nieujemną zapisuje się jako 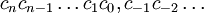 . W krajach anglosaskich zamiast przecinka zarezerwowanego do oddzielania tysięcy używana jest kropka. Dla liczb ujemnych zapisujemy ich
moduł
, dodając z przodu znak − , np. − 25,4[9]. Przez analogię dla liczb dodatnich można dodać z przodu znak + . W
księgowości
stosuje się też inne notacje, np. liczby ujemne ujmuje się w nawiasy.
. W krajach anglosaskich zamiast przecinka zarezerwowanego do oddzielania tysięcy używana jest kropka. Dla liczb ujemnych zapisujemy ich
moduł
, dodając z przodu znak − , np. − 25,4[9]. Przez analogię dla liczb dodatnich można dodać z przodu znak + . W
księgowości
stosuje się też inne notacje, np. liczby ujemne ujmuje się w nawiasy.
Liczby rzeczywiste często wymagają nieskończonej liczby cyfr do swego zapisu. Zapis liczb wymiernych zawsze wykazuje okresowość, tzn. począwszy od pewnego momentu ciąg cyfr zaczyna się cyklicznie powtarzać. Liczby naturalne są zapisywane skończoną liczbą cyfr, gdyż wszystkie cyfry ci dla i < 0 są zerami, więc ich zapis można pominąć.
Addytywne systemy liczbowe
W
addytywnych systemach liczbowych
symbole mają zawsze tę samą wartość, a liczbę uzyskuje się przez ich sumowanie. Tym samym musi ich być odpowiednio więcej. Przykłady:
Reprezentacje liczb w informatyce
Dane w
pamięci komputera
czy też w plikach zapisane są w postaci ciągu tzw.
bajtów
. Każdy bajt składa się z ośmiu cyfr systemu dwójkowego (0 lub 1), zwanych
bitami
. Pojedynczy bajt może przyjmować jeden z 28 = 256 stanów. Powstaje konieczność zakodowania liczb w postaci ciągu bajtów, tak aby komputery mogły je przetwarzać. Można to zrobić na wiele sposobów, jednak w praktyce używanych jest kilka standardów:
Liczby naturalne
Typ
obejmujący przedział liczb naturalnych z zerem zwany jest w informatyce liczbami bez znaku (ang. unsigned integers). W informatyce zawsze zalicza się zero do liczb bez znaku i – w odróżnieniu od matematyki – elementy
ciągu
, zwanego tu
tablicą jednowymiarową
, w najpopularniejszych
językach
numeruje się konsekwentnie od zera[10].
Liczby naturalne z przedziału 0-255 można po prostu zakodować jako wartość jednego bajta.
Na dwóch bajtach można już zapisać liczby naturalne z przedziału 0-65535 (mamy do dyspozycji 65536 = 2562 stanów). Każdą taką liczbę można zapisać w postaci x = 256h + l, gdzie h oraz l to wartości tzw. starszego bajta i młodszego bajta, z przedziału od 0 do 255 każda. Wartości te można zapisać w pamięci na dwa sposoby: albo pierwszy jest starszy bajt, a drugi młodszy (tzw. notacja
big endian
), albo odwrotnie (
little endian
). W procesorach kompatybilnych z architekturą
Intela
(czyli np. w komputerach
PC
) stosowany jest little endian, a w wielu innych procesorach (np. na większości serwerów) big endian. Są też procesory na których kolejność można przełączać. Nie ma to wielkiego znaczenia, dopóki nie zapiszemy liczby do
pliku
, albo nie prześlemy jej siecią i nie przeniesiemy w ten sposób na komputer stosujący inny standard. Z tego powodu np. maszyny wirtualne
Java
wykorzystują w plikach format big endian niezależnie od procesora.
Na czterech bajtach można zapisać liczby z przedziału 0 – 4 294 967 295. Analogicznie jak poprzednio, przedstawienie danej liczby w systemie 256-kowym pozycyjnym jako x = 2563a3 + 2562a2 + 256a1 + a0 uzyskuje się cztery bajty a3,a2,a1,a0. Kolejność ich zapisu w pamięci, tak jak poprzednio, zależy od procesora – w przypadku little endian od bajta a0 do a3, w przypadku big endian – odwrotnie.
Do niektórych zastosowań konieczne są jeszcze większe liczby naturalne, np. zapisywane na 8 bajtach (w rodzinie C oznaczane unsigned _int64 lub unsigned long long int).
Istnieją inne sposoby zapisu liczb naturalnych, bardzo rzadko jednak stosowane. Należy do nich
kod BCD
(od ang. binary coded decimal), gdzie kolejne cyfry dziesiętne są zapisywane w kolejnych półbajtach (inaczej niblach, porcjach danych długości 4 bitów). Komplikuje to arytmetykę, ale upraszcza przeliczanie na system dziesiętny, kod BCD jest więc czasem stosowany w licznikach cyfrowych.
Liczby całkowite
Typ obejmujący przedział liczb całkowitych zwany jest w informatyce liczbami ze znakiem (ang. signed integers).
Stosuje się tzw.
kod uzupełnień do dwóch
(U2). Liczba x, która ma zostać zapisana w postaci n bajtów jest przekształcana w następujący sposób:
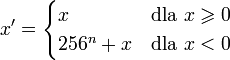
Następnie liczba x' jest zapisywana jako liczba naturalna. W ten sposób na jednym bajcie można zapisywać liczby z przedziału od − 128 do 127, na dwóch od − 32768 do 32767, i ogólnie na n bajtach liczby od − 28n − 1 do 28n − 1 − 1 włącznie.
Istnieją inne metody zapisu (np.
kod uzupełnień do jedności
), obecnie jednak nie stosowane.
W celu zapisywania dużych liczb naturalnych lub całkowitych buduje się odpowiednie
klasy
, np. java.math.BigInteger w języku
Java
[11]
Liczby rzeczywiste
Liczby rzeczywiste mogą być zapisywane jako:
Powszechnie stosuje się zmiennoprzecinkowy zapis liczby rzeczywistej w standardzie
IEEE 754
. Przybliżenie liczby rzeczywistej jest zapisywane w postaci 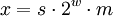 , gdzie
, gdzie  jest nazywany znakiem, w – wykładnikiem, a
jest nazywany znakiem, w – wykładnikiem, a  – mantysą. Zero, które można by zakodować na wiele sposobów jest kodowane jako s = + 1,w = 0,m = 0
– mantysą. Zero, które można by zakodować na wiele sposobów jest kodowane jako s = + 1,w = 0,m = 0
Znak jest zapisywany jako jeden bit, równy 0 dla s = + 1 i 1 dla s = − 1. Wykładnik jest zapisywany jak każda inna liczba całkowita w kodzie uzupełnień do dwóch. Mantysa jest mnożona przez 2f, gdzie f to liczba bitów przeznaczona na nią i zapisywana jako liczba naturalna.
Całość zajmuje kolejnych 4, 8 albo 16 bajtów (w zależności od wymaganej precyzji). Ich kolejność umieszczenia w pamięci jest zależna od procesora, identycznie jak w przypadku liczb naturalnych i całkowitych.
Liczby zespolone i kwaterniony
Niektóre
języki programowania
posiadają arytmetykę liczb zespolonych. W nowoczesnych językach zwykle jest to realizowane za pomocą odpowiednich klas, np. Complex ze standardowej biblioteki
C++
. Jedną z przyczyn dawnej popularności
Fortrana
był fakt, iż język ten jako pierwszy posiadał
typ
liczb zespolonych.
Klasa obsługująca kwaterniony zdefiniowana jest w pakiecie
DirectX
[12], będąc sposobem na użycie tzw.
współrzędnych jednorodnych
do opisu
punktów
modelowanej
przestrzeni
trójwymiarowej
(
wierzchołków
trójwymiarowej sceny) w
grafice trójwymiarowej
; podobne typy istnieją również w innych pakietach grafiki trójwymiarowej.
Historia
Przypisy
- ↑ np.
fraktale
- ↑ zob.
zastosowanie liczb zespolonych w analizie obwodów elektrycznych
, ponadto stosowane są one również w teorii sygnałów
- ↑ np.
funkcja falowa
- ↑ Dopiero w
XVII wieku
zero było powszechnie rozpoznawane jako liczba w Europie. Źródło:
http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Zero.html
- ↑ Zdaniem pitagorejczyków odkrycie to zaprzeczało głoszonej przez nich doskonałości wszelkich liczb – liczby niewymierne uznali za niedoskonałe. Zobacz też
dowód niewymierności pierwiastka z dwóch
.
- ↑
Witold Więsław
stwierdza: Pitagorejczycy udowodnili, że przekątna kwadratu nie jest współmierna z jego bokiem, tzn.
 jest liczbą niewymierną. Byłoby interesujące dowiedzieć się, kto pierwszy tego dowiódł. Zapewne nigdy się już tego nie dowiemy. Jedno jest pewne: Pitagoras pod koniec V w. p.n.e. wiedział, że
jest liczbą niewymierną. Byłoby interesujące dowiedzieć się, kto pierwszy tego dowiódł. Zapewne nigdy się już tego nie dowiemy. Jedno jest pewne: Pitagoras pod koniec V w. p.n.e. wiedział, że  jest liczbą niewymierną. (Zob.: Więsław, Witold: Matematyka i jej historia, Wydawnictwo NOWIK, Opole 1997, , strona 36.)
jest liczbą niewymierną. (Zob.: Więsław, Witold: Matematyka i jej historia, Wydawnictwo NOWIK, Opole 1997, , strona 36.) - ↑ Weisstein, Eric W.:
Rational Number in MathWorld – A Wolfram Web Resource
. [dostęp 12 kwietnia 2007].
- ↑ co udowodnił
Georg Cantor
w 1874; zobacz też
twierdzenie Cantora
- ↑ Typografia wyróżnia cztery różne znaki: - (
dywiz, łącznik
), – (
półpauza
), — (
pauza
) oraz − (
minus
), który od półpauzy różni się wyglądem oraz położeniem (zgodnym z innymi znakami matematycznymi).
- ↑ np. w
C
,
C++
,
Java
,
JavaScript
,
C#
, w
asemblerach
,
PHP
(przy wywołaniu funkcji
array z domyślnymi parametrami),
Perl
, choć istnieją starsze języki w których numeruje się je od jedynki (wiele dialektów
Basica
,
Fortran
), lub zakres numeracji można samodzielnie zdefiniować (
Pascal
,
SAS 4GL
,
Algol
,
Ada
) - ↑ Dokumentacja:
http://java.sun.com/j2se/1.4.2/docs/api/java/math/BigInteger.html
- ↑ Dokumentacja:
http://msdn2.microsoft.com/en-us/library/microsoft.windowsmobile.directx.quaternion.aspx
Bibliografia
- Jerzy Klukowski, I. Nabiałek: Algebra dla studentów. Wyd. 4. 2004. .
-
Franciszek Leja
: Rachunek różniczkowy i całkowy. Warszawa: PWN, 1976.
-
Krzysztof Maurin
: Analiza – Część I – Elementy. Warszawa: PWN, 1976.
- Helena Musielak, Julian Musielak: Analiza matematyczna. Poznań: Wydawnictwo Naukowe UAM, 2000. .
- Fritz Reinhardt, Heinrich Soeder: Atlas matematyki. Prószyński i S-ka, 2003. .
- Jerzy Rutkowski: Algebra abstrakcyjna w zadaniach. Wyd. 5. 2006. .
- J. Widomski: Ontologia liczby. Kraków: 1996.
Wyprowadzenie wszystkich algebr liczbowych od liczb naturalnych do oktaw Cayleya włącznie, w sposób zrozumiały dla uczniów gimnazjum, znajduje się w książce:
-
Bogdan Miś
: Tajemnicza liczba e i inne sekrety matematyki. Warszawa: Wydawnictwa Naukowo-Techniczne, 1989.
Zobacz też
liczby
-
algebraiczne
,
-
automorficzne
,
-
bliźniacze
,
-
całkowite
,
-
doskonałe
,
-
dualne
-
Fermata
,
-
Fibonacciego
,
-
kardynalne
,
-
Mersenne'a
,
-
naturalne
,
-
niewymierne
,
-
p-adyczne
,
-
parzyste i nieparzyste
,
-
pierwsze
,
| -
piramidalne
,
-
podobieństwa
,
-
podwójne
,
-
porządkowe
,
-
półpierwsze
,
-
przestępne
,
-
rzeczywiste
,
-
ujemne
,
-
urojone
,
-
wymierne
-
zaprzyjaźnione
,
-
zespolone
,
-
złożone
,
-
kwaterniony
,
-
oktawy Cayleya
.
|