Pole powierzchni (potocznie po prostu powierzchnia figury lub pole figury) - miara , przyporządkowująca danej figurze nieujemną liczbę w pewnym sensie charakteryzującą jej rozmiar.

Ścisła definicja wymaga wykonania pewnej konstrukcji.

Konstrukcja pojęcia pola

I Definicja

Najczęściej spotykana definicja (i jedna z najogólniejszych) odwołuje się do następującej konstrukcji:

1. Pokrywamy całą płaszczyznę , na której znajduje się dana figura, siatką przylegających kwadratów o bokach a₁.
2. Liczbę kwadratów mających choćby jeden punkt wspólny z figurą, której powierzchnię mierzymy, oznaczamy przez n₁.

Tworząc rozmaite siatki kwadratów o coraz mniejszych bokach , itd. uzyskujemy ciąg liczb n₁,n₂,....
Polem powierzchni nazywamy granicę :

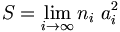
Granica ta nie zawsze istnieje. Jeśli nie istnieje, pola powierzchni nie da się obliczyć tą metodą.

Co więcej, konstrukcja ta ma jeszcze jedną wadę - choć dobrze sprawdza się w typowych wypadkach, jednak nie ma podstawowej własności, która intuicyjnie powinna charakteryzować pole powierzchni: suma pól dwóch rozłącznych figur może być większa niż pole figury powstałej z ich połączenia.

Problem wyznaczania pól dla wszystkich figur

• Zbiory

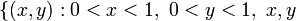są wymierne oraz

jest niewymierny lub jest niewymierny

są rozłączne i oba mają zewnętrzną miarę Jordana równą 1. Suma tych dwóch figur (czyli wnętrze kwadratu) ma pole równe 1, skąd możemy wnioskować że pola naszych figur nie można zdefiniować używając podejścia Jordana.

• Istnienie nietrywialnej funkcji , którą dałoby się zmierzyć dowolną figurę i która dla dowolnego ciągu przeliczalnego rozłącznych figur dawałaby wynik równy ich sumie jest niedowodliwe w standardowym systemie aksjomatów ZFC .
• Zbiór Vitalego i zbiór Bernsteina (istniejące przy założeniu aksjomatu wyboru ) są niemierzalne w sensie Lebesgue'a.
• Przy założeniu aksjomatu wyboru istnieje skończenie addytywna miara mierząca wszystkie podzbiory przestrzeni.
• Przy założeniu AD , wszystkie podzbiory przestrzeni euklidesowych są mierzalne w sensie Lebesgue'a.
• Jeśli istnieje liczba mierzalna , to jest niesprzeczne że continuum jest rzeczywiście mierzalne i że istnieje miara na płaszczyźnie mierząca wszystkie jej podzbiory.

Definicja szkolna

Definicja używana w gimnazjach i szkołach średnich.

1. Obieramy kwadrat o boku 1.
2. Kwadrat ten zwany kwadratem jednostkowym jest jednostką pola.
3. Pole jest równe liczbie kwadratów jednostkowych lub jego części mieszczących się całkowicie w mierzonej figurze.

Definicja ta podaje tylko dolne oszacowanie pola powierzchni danej figury, którego dokładność zależy od kształtu figury.

Pole pod krzywą

Pole między krzywą daną równaniem y=f(x) a osią OX ograniczone prostymi x=a i x=b, a≤b jest równe całce oznaczonej

Pola typowych figur

• Równoległobok o bokach a i b oraz kącie α między nimi:
  • Prostokąt o bokach a i b: ; o przekątnej p i stosunku proporcji boków ratio:
  • Kwadrat o boku a: ; o przekątnej p:
• pole obszaru ograniczonego przez elipsę o półosiach a i b:
• Koło o promieniu r:
• Trójkąt o podstawie a, wysokości h i kącie α między bokami c i d:
• Wielokąt foremny (n - liczba boków, r – promień okręgu wpisanego w wielokąt, R – promień okręgu opisanego , a – bok wielokąta):

• Trójkąt równoboczny :

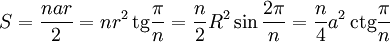
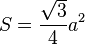
Zobacz też

• Wzór Picka