Filtr to pojęcie używane w matematyce , głównie w teorii porządków częściowych , teorii algebr Boole'a , topologii i teorii mnogości .

Intuicje

Wśród realizacji najogólniejszej definicji filtru (formułowanej dla porządków częściowych) są filtry jako rodziny zbiorów . Odpowiednią intuicją wtedy jest, że filtr to rodzina zbiorów w jakimś sensie dużych. Wydaje się naturalnym, że pojęcie dużych zbiorów powinno spełniać pewne podstawowe własności:

• zbiór większy od dużego zbioru powinien być duży,
• zbiór pusty nie powinien być duży ale cała przestrzeń ( uniwersum ) powinna być duża,
• część wspólna dwóch dużych zbiorów powinna być duża.

Rodzina zbiorów spełniająca powyższe wymagania (jako rodzina zbiorów dużych) jest właśnie filtrem zbiorów, patrz poniżej.

Definicje

Filtry w porządkach

Niech 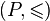będzie porządkiem częściowym. Powiemy, że zbiór 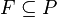jest filtrem w zbiorze uporządkowanym P jeśli następujące warunki są spełnione:

(i) ,

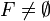(ii) jeśli , 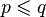oraz , to również ,

(iii) jeśli , to można znaleźć taki że 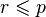oraz .

Filtr F jest właściwy jeśli dodatkowo

(iv) .

Jeśli porządek 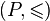jest półkratą dolną (dla każdych p, q istnieje kres dolny 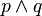), to warunki (ii)+(iii) są równoważne z warunkiem

(v) dla każdych : 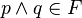wtedy i tylko wtedy, gdy ( i ).

Filtry w algebrach Boole'a

Ponieważ algebra Boole'a jest także zbiorem częściowo uporządkowanym, to definicja filtru na porządkach częściowych może być przeniesiona bez zmian na algebry Boole'a. Możemy jednak wykorzystać fakt, że porządek boole'owski jest związany z operacjami algebry i możemy sformułować definicję filtru trochę inaczej.

Niech 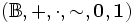będzie algebrą Boole'a. Powiemy, że zbiór F jest filtrem w algebrze Boole'a jeśli następujące warunki są spełnione:

(i) ,

(ii) jeśli , 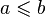(tzn ) oraz 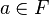, to również ,

(iii) jeśli 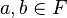, to .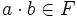

Filtr F jest właściwy jeśli dodatkowo

(iv) .

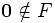Należy podkreślić, że powyższa definicja i ta przeniesiona z porządków częściowych są równoważne.

Filtry podzbiorów danego zbioru

Szczególnym przypadkiem algebry Boole'a jest rodzina wszystkich podzbiorów ustalonego zbioru S (z operacjami sumy , przekroju i dopełnienia zbiorów). Zatem sformułowana powyżej definicja filtru w algebrze Boole'a może być powtórzona bez zmian dla podzbiorów zbioru S. Sformułujemy tę definicję jeszcze raz dla podkreślenia znaczenia intuicji, że filtr to rodzina dużych podzbiorów S.

Niech S będzie niepustym zbiorem. Powiemy, że rodzina F podzbiorów zbioru S jest filtrem podzbiorów zbioru S jeśli następujące warunki są spełnione:

(i) ,

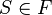(ii) jeśl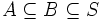i i 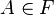, to również ,

(iii) jeśli 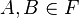, to .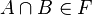

Filtr F jest właściwy jeśli dodatkowo

(iv) .

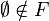Mówimy, że filtr F podzbiorów liczby kardynalnej κ jest jednorodny, gdy , tzn. filtr F nie zawiera podzbiorów zbioru κ mocy mniejszej niż κ.

Charakterem filtru nazywamy liczbę

Filtry maksymalne

Filtr właściwy F w porządku częściowym 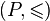jest filtrem maksymalnym jeśli jedynym filtrem właściwym zawierającym F jest samo F.

Filtry maksymalne są też często nazywane ultrafiltrami, szczególnie w odniesieniu do filtrów w algebrach Boole'a i filtrów podzbiorów danego zbioru.

Filtry pierwszy

Filtr właściwy F w górnym pólkracie 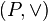jest filtrem pierwszym jeśli następujący warunek jest spełniony:

• dla każdych : ( albo ).

Innymi słowy, filtr F jest filtrem pierwszym wtedy i tylko wtedy, gdy zbior 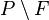jest ideałem.

Jeśli P jest porządkiem liniowym, to każdy filtr jest filtrem pierwszym. Jeśli P jest kratą rozdzielną , to każdy filtr maksymalny jest filtrem pierwszym.

Jeśli F jest właściwym filtrem w algebrze Boole'a B, następujące warunki są równoważne:

• F jest filtrem maksymalnym
• F jest filtrem pierwszym
• dla każdego b w algebrze B: .

Przykłady

Filtry w algebrach Boole'a

• Rodzina tych borelowskich podzbiorów odcinka [0,1], które mają miarę Lebesgue'a równą 1 jest filtrem w algebrze borelowskich podzbiorów odcinka.

Filtry podzbiorów danego zbioru

• Niech S będzie zbiorem nieskończonym. Rodzina tych podzbiorów S które mają dopełnienie skończone jest filtrem podzbiorów S. Jest on często nazywany filtrem Frécheta .
• Rodzina tych podzbiorów odcinka [0,1] które mają miarę Lebesgue'a 1 jest filtrem podzbiorów [0,1].
• Jeśli jest rodziną podzbiorów zbioru X z własnością skończonych przekrojów , to zbiór

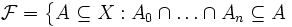dla pewnych ,

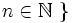
jest filtrem podzbiorów X.

• Niech . Wówczas jest filtrem podzbiorów X. Filtry tej postaci są nazywane filtrami głównymi i zwykle nie są one obiektem rozważań (tzn typowym założeniem o rozważanych filtrach jest że są one niegłówne).
• Niech κ będzie nieprzeliczalną regularną liczbą kardynalną . Rozważmy rodzinę domkniętych nieograniczonych podzbiorów κ: jest ona zamknięta na przekroje mocy mniejszej niż κ. Zatem jest filtrem (właściwym) podzbiorów κ.

Własności i zastosowania

• Każdy właściwy filtr w algebrze Boole'a jest zawarty w pewnym filtrze maksymalnym (ultrafiltrze). (To twierdzenie, udowodnione przez Tarskiego , wymaga pewnej formy AC .)
• Twierdzenie Stone'a mówi, że każda algebra Boole'a jest izomorficzna z ciałem otwarto-domkniętych podzbiorów swojej przestrzeni ultrafiltrów.
• Jeśli F jest filtrem w algebrze Boole'a 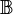, to 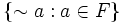jest ideałem tej algebry.
• Filtry w częściowych porządkach są używane w teorii forsingu . Są one również kluczowe w sformułowaniach aksjomatów takich jak Aksjomat Martina .
• Ultrafiltry są używane w teorii modeli przy tworzeniu ultraproduktów modeli i jako takie mają duże znaczenie w tej dziedzinie matematyki. Okazały się one też być bardzo ważnymi w topologii, gdzie są używane do opisu uzwarceń przestrzeni topologicznych . W tym ostatnim kontekście ultrafiltry na zbiorze liczb naturalnych były intensywnie badane w drugiej polowie XX wieku jako elementy uzwarcenia Čecha-Stone'a zbioru liczb naturalnych .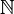
• Zupełne ultrafiltry są podstawą w rozważaniach dużych liczb kardynalnych . Filtr F podzbiorów zbioru S jest κ-zupełny jeśli przekrój mniej niż κ zbiorów z F należy do F. Liczba kardynalna κ jest mierzalna jeśli istnieje κ-zupełny niegłówny ultrafiltr podzbiorów κ. Liczby mierzalne są punktem wyjściowym dla hierarchii dużych liczb kardynalnych.

Zobacz też

• Ideał
• Aksjomat Martina