Fale na wodzie

Fala morska

Fala - zaburzenie rozprzestrzeniające się w ośrodku lub przestrzeni . Fale przenoszą energię z jednego miejsca do drugiego bez transportu jakiejkolwiek materii . W przypadku fal mechanicznych cząstki ośrodka, w którym rozchodzi się fala, oscylują wokół położenia równowagi .

Charakterystyczne własności

Wszystkie fale wykazują następujące własności:

• prostoliniowe rozchodzenie się fali w ośrodkach jednorodnych ,
• odbicie – po dojściu do granicy ośrodków fale zmieniają kierunek poruszając się nadal w tym samym ośrodku
• załamanie – na granicy ośrodków fala przechodząc do ośrodka, w którym porusza się z inną prędkością, zmienia kierunek swego biegu,
• dyfrakcja – uginanie się fali na krawędziach, czego skutkiem jest zdolność do omijania przeszkód mniejszych niż długość fali , oraz powstawanie pasków dyfrakcyjnych po przejściu fali przez wąską szczelinę albo przeszkodę;

Rozchodzące fale nakładają się na siebie w wyniku czego zachodzą zjawiska:

• interferencja – nakładanie się spójnych fal z różnych źródeł, które prowadzi do wzmocnienia lub wygaszenia się fal;
• dudnienie – oscylacje amplitudy fali;

Fale o różnych długościach mogą w różnych ośrodkach rozchodzić się z różnymi prędkościami. Efekt ten, nazywamy dyspersją fali , powoduje na przykład:

• rozszczepienie – załamanie fal pod różnymi kątami, zależnie od ich długości, powoduje rozkład fali na fale składowe, np. rozszczepienie światła w pryzmacie .

Fale poprzeczne i podłużne

Fale poprzeczne mają kierunek drgań prostopadły do kierunku rozchodzenia się (np. fale morskie, fale elektromagnetyczne ). W falach podłużnych drgania odbywają się w tym samym kierunku, w którym następuje ich propagacja (np. fale dźwiękowe).

Polaryzacja

Fale poprzeczne mogą być spolaryzowane, co oznacza, że kierunek drgań jest w pewien sposób uporządkowany, na przykład odbywają się one w jednej płaszczyźnie (polaryzacja liniowa). Fale radiowe generowane przez anteny są spolaryzowane. Większość źródeł fal świetlnych generuje fale niespolaryzowane, w których drgania w różnych kierunkach się nakładają.

Matematyczny opis fali

Matematycznie fala to rozwiązanie równania falowego . Jest to dowolna funkcja różniczkowalna spełniająca to równanie. Rozwiązania równania falowego tworzą przestrzeń liniową , która jest przestrzenią Hilberta . Jako bazę tej przestrzeni można wybrać drgania podstawowe w postaci przebiegów harmonicznych (dla prostokątnego układu współrzędnych, w wypadku innych symetrii zjawiska właściwsze stają się inne bazy, jak np. harmoniki sferyczne czy bardziej skomplikowane funkcje specjalne ). Dowolne rozwiązanie równania falowego, a więc dowolną falę można przedstawić jako sumę szeregu funkcji bazowych, a więc przebiegów harmonicznych, co jest zasadą analizy harmonicznej odkrytej przez Fouriera .

Fala harmoniczna

Fala harmoniczna

Najprostszym rodzajem fali jest fala harmoniczna biegnąca, zwana też falą sinusoidalną, rozchodząca się w ośrodku jednowymiarowym (np. lince).

Falę taką opisuje równanie fali biegnącej, które jest rozwiązaniem równania falowego w jednym wymiarze (wzdłuż np. osi z). Wielkością drgającą jest pewna wielkość fizyczna y (np. wysokość nad poziomem morza, gęstość, natężenie pola elektrycznego). Dla fali o okresie T i długości λ rozwiązanie równania falowego można przedstawić w postaci^[1]:

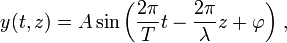
co może być zapisane prościej, przyjmując:

gdzie:

• A – amplituda fali,
• T – okres drgań ,
• λ – długość fali,
• ω – częstość kołowa zwana krótko częstością lub pulsacją fali, ,
• k – liczba falowa ,
• φ – faza początkowa

Argument funkcji sinus   to faza fali .

Punkt o danej fazie porusza się z prędkością, zwaną prędkością fazową :

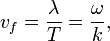
Jeżeli amplituda fali zmienia się, to zmiana amplitudy może rozchodzić się z inną prędkością niż prędkość fazowa. Prędkość rozchodzenia zmiany amplitudy nazywana jest prędkością grupową fali v_g określona jest wzorem:

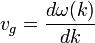
Z prędkością zmiany amplitudy (czoła fali) poruszają się modulacje fali, oznacza to że informacje przenoszone przez falę rozchodzą się z prędkością grupową. Jeżeli prędkość fazowa nie zależy od liczby falowej fali, prędkość fazowa i grupowa są sobie równe a falę taką określa się jako niedyspersyjną, w przeciwnym przypadku fala ulega zjawiskom z tym związanym zwanymi dyspersją .

W ośrodkach wielowymiarowych kształt czoła fali zależy od warunków jej wytworzenia. Może być np. płaszczyzną ( fala płaska ), kołem (fala kolista) powierzchnią kuli ( fala kulista ) a nawet stożkiem (gdy źródło fali porusza się z prędkością większą od prędkości grupowej).

Zobacz też

• efekt Dopplera
• fala uderzeniowa
• zasada Huygensa

Przypisy

Bibliografia