Transformacja Lorentza (przekształcenie Lorentza) –
przekształcenie liniowe
przestrzeni Minkowskiego
umożliwiające obliczenie wielkości fizycznych w pewnym układzie odniesienia, jeśli znane są te wielkości w układzie poruszającym się względem pierwszego. Przekształceniu temu podlegają np. współrzędne w czasoprzestrzeni, energia i pęd, prędkość (zarówno wartość jak i kierunek), pole elektryczne i magnetyczne. Wzory transformacyjne zostały wyprowadzone przez
Lorentza
w oparciu o założenie, że prędkość światła jest stała i niezależna od prędkości układu. Bardziej ogólną transformacją czasoprzestrzeni jest transformacja Poincarego.
Transformacja współrzędnych
Transformacja Lorentza zachowuje odległości w czasoprzestrzeni. W przeciwieństwie do
transformacji Galileusza
, gdzie niezmiennikiem jest czas i odległość w przestrzeni, w transformacji Lorentza zachowany jest
interwał
(odległość zdarzeń w czasoprzestrzeni), podczas gdy wielkość jednostki czasu i odległości zależy od prędkości układu odniesienia.
Transformacje współrzędnych mają najprostszą postać wówczas, gdy odpowiadające sobie osie współrzędnych kartezjańskich inercjalnych układów odniesienia, nieruchomego K i poruszającego się K', są do siebie wzajemnie równoległe, przy czym układ K' porusza się ze stałą prędkością  wzdłuż osi OX. Jeśli ponadto jako początek odliczania czasu w obu układach (t = 0) i (t' = 0) wybrany został moment, w którym początki osi współrzędnych O i O' w obu układach pokrywają się, to transformacje Lorentza są w postaci:
wzdłuż osi OX. Jeśli ponadto jako początek odliczania czasu w obu układach (t = 0) i (t' = 0) wybrany został moment, w którym początki osi współrzędnych O i O' w obu układach pokrywają się, to transformacje Lorentza są w postaci:

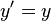


gdzie
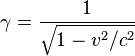
lub inaczej


Dla prędkości znacznie mniejszych od prędkości światła  i
i  , transformacja Lorentza staje się równoważna z transformacją Galileusza. Oznacza to, że ta druga jest przybliżeniem transformacji Lorentza dla małych prędkości.
, transformacja Lorentza staje się równoważna z transformacją Galileusza. Oznacza to, że ta druga jest przybliżeniem transformacji Lorentza dla małych prędkości.
W uogólnieniu macierzowym
Rozpatrujemy
czterowektory
, których jedną współrzędną (numerowaną od 0) jest składowa czasowa jakiejś wielkości, a pozostałymi trzema współrzędnymi - klasyczne składowe przestrzenne. W wartościach współrzędnych czterowektorów kryje się wybór konkretnego układu współrzędnych. Aby uzyskać współrzędne interesujących nas wektorów w innym układzie, należy dokonać transformacji (stosujemy
konwencję sumacyjną Einsteina
):

gdzie:
 - wektor w oryginalnym układzie współrzędnych
- wektor w oryginalnym układzie współrzędnych - wektor w nowym układzie współrzędnych
- wektor w nowym układzie współrzędnych - przekształcenie między starym a nowym układem współrzędnych.
- przekształcenie między starym a nowym układem współrzędnych.
Tensorem metrycznym
(metryką) przestrzeni Minkowskiego jest macierz 4x4 której składową (0,0) jest -1, pozostałymi składowymi diagonalnymi jest 1, a wszystkimi innymi składowymi - 0. Metrykę oznaczamy literą g. Aby przekształcenie było transformacją Lorentza, musi pozostawiać metrykę niezmienioną, a wyznacznik jego macierzy musi wynosić 1 lub -1.

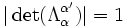
Podgrupy
Jeżeli zażądamy, żeby wyznacznik macierzy przekształcenia Lorentza był równy dokładnie 1, uzyskamy grupę Lorentza bez odbić przestrzennych.
Przekształcenie Lorentza, którego wszystkie współrzędne z wymiarem czasowym są równe 0, z wyjątkiem elementu diagonalnego, który jest równy 1, nazywamy obrotem.
Przekształcenie Lorentza, którego wszystkie współrzędne bez wymiaru czasowego są równe 0, z wyjątkiem elementów diagonalnych, które są równe 1, nazywamy pchnięciem. Pchnięcie przekształca układ współrzędnych w układ poruszający się względem oryginalnego ze stałą prędkością.
Przekształcenia Lorentza bez przesunięć (translacji), czyli takie, które przekształcają początek układu współrzędnych w samego siebie, nazywane są jednorodnymi przekształceniami Lorentza. Przekształcenia Lorentza rozpatrywane razem z przesunięciami nazywają się niejednorodnymi przekształceniami Lorentza.
Wyprowadzenie zjawisk relatywistycznych
Z równań transformacji Lorentza można wyprowadzić wszystkie zjawiska szczególnej teorii względności a także wielkości składowych pól elektrycznego i magnetycznego, które zmieniają się przy zmianie układu odniesienia, jak również określają dodatkowe niezmienniki.
Skrócenie Lorentza-Fitzgeralda
Istotna dla nas dwuwymiarowa czasoprzestrzeń z perspektywy układu Bx',t' w porównaniu z układem Ax,t jest opisana następującymi równaniami:


Przez długość rozumiemy odległość dwóch punktów x'1, x'2 na osi OX' w tej samej chwili t' (ponieważ mierzone ciało jest częścią A, więc z perspektywy B jest w ruchu wzdłuż OX', stąd konieczność zagwarantowania względnie jednoczesnego pomiaru). Najpierw wyrazimy x' za pomocą t':
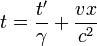



Obliczmy długość L' (zał. t'1 = t'2):
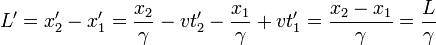
Ponieważ γ > 1, więc ciało o długości spoczynkowej L zmierzonej w układzie A jest z perspektywy układu B krótsze, co potwierdza relatywistyczną kontrakcję.
Dylatacja czasu
Odejmując wyrażenia na transformację Lorentza dla dwu zdarzeń czasoprzestrzennych i definiując przyrosty czasu w każdym z układów odniesienia jako jednostki czasu mierzonego w danym układzie można uzyskać równanie:
 .
.
We wzorze pojawia się dodatkowo różnica odległości w jednym z układów. Zinterpretowanie tej różnicy jako równej zeru powoduje, że porównuje się współrzędne czasowe wyłącznie jednego zdarzenia, ale w dwu układach odniesienia. Uzyskany wzór określa zatem dylatację czasu (γ > 1).
Pole magnetyczne
W teoriach relatywistycznych skalar natężenia pola elektrycznego (E0) i wektor natężenia pola magnetycznego (B) można połączyć w jeden czterowektor (E).
![E = [E_0, c B_1, c B_2, c B_3]\,](http://upload.wikimedia.org/math/c/7/2/c7265142c55cffcc8dac99d455f2ed0a.png)
Rozważmy cząstkę skalarną naładowaną elektrycznie i pozostającą w bezruchu. W pewnej odległości od tej cząstki zarejestrujemy pole elektryczne i brak pola magnetycznego.

![B = [0, 0, 0]\,](http://upload.wikimedia.org/math/9/8/1/981952c37659bf1da9cb49ec5951e31b.png)
Załóżmy następnie, że naładowana cząstka się porusza, czyli zmieniamy układ współrzędnych na poruszający się względem pierwszego wzdłuż pierwszej osi z prędkością v.
- E'0 = γ(E0 − vcB1) = γE0

Czyli poruszający się ładunek generuje pole magnetyczne.
Czynnik γ jest dla małych prędkości bliski jedności, więc w granicy małych prędkości transformacje Lorentza czterowektora pola elektrycznego sprowadzają się do
praw Ampera
i
Biota-Savarta
.